题目内容
已知函数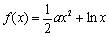 ,
,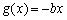 ,设
,设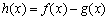 .
.
(1)若 在
在 处取得极值,且
处取得极值,且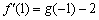 ,求函数h(x)的单调区间;
,求函数h(x)的单调区间;
(2)若 时函数h(x)有两个不同的零点x1,x2.
时函数h(x)有两个不同的零点x1,x2.
①求b的取值范围;②求证: .
.
(1)因为 ,所以
,所以 ,
,
由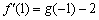 可得a=b-3.
可得a=b-3.
又因为 在
在 处取得极值,
处取得极值,
所以 ,
,
所以a= -2,b=1 .
所以 ,其定义域为(0,+
,其定义域为(0,+ )
)

令 得
得 ,
,
当 (0,1)时,
(0,1)时, ,当
,当 (1,+
(1,+ )
) ,
,
所以函数h(x)在区间(0,1)上单调增;在区间(1,+ )上单调减.
)上单调减.
(2)当 时,
时, ,其定义域为(0,+
,其定义域为(0,+ ).
).
①由 得
得 ,记
,记 ,则
,则 ,
,
所以 在
在 单调减,在
单调减,在 单调增,
单调增,
所以当 时
时 取得最小值
取得最小值 .
.
又 ,所以
,所以 时
时 ,而
,而 时
时 ,
,
所以b的取值范围是( ,0).
,0).
②由题意得 ,
,
所以 ,
,
所以 ,不妨设x1<x2,
,不妨设x1<x2,
要证 , 只需要证
, 只需要证 .
.
即证 ,设
,设 ,
,
则 ,
,
所以 ,
,
所以函数 在(1,+
在(1,+ )上单调增,而
)上单调增,而 ,
,
所以 即
即 ,
,
所以 .
.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 ,
, ,其中
,其中 是虚数单位,则
是虚数单位,则 .
.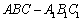 中,侧面
中,侧面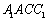 是边长为
是边长为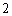 的菱形,
的菱形,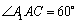 .在面
.在面 中,
中,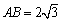 ,
,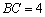 ,
,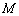 为
为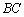 的中点,过
的中点,过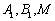 三点的平面交
三点的平面交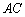 于点
于点 .
.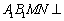 平面
平面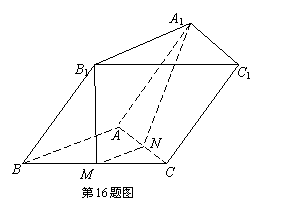
 在
在 处取得最值的概率是 .
处取得最值的概率是 . 上的奇函数,若当
上的奇函数,若当 时,
时, ,则关于
,则关于 的函
的函 的所有零点之和为 (用
的所有零点之和为 (用 表示)
表示) ,
, ,求a的取值范围.
,求a的取值范围.
 满足:
满足: .
. 在矩阵
在矩阵 ,求曲线
,求曲线 在点
在点 处的切线方程为________.
处的切线方程为________.