题目内容
已知直线l:x-2y+4=0和两点A(0,4),B(-2,-4),点P(m,n)在直线l上有移动.
(1)求m2+n2的最小值;
(2)求||PB|-|PA||的最大值.
(1)求m2+n2的最小值;
(2)求||PB|-|PA||的最大值.
考点:两点间距离公式的应用
专题:计算题,直线与圆
分析:(1)点P(m,n)在直线l上有移动,可得m2+n2的最小值为原点到直线距离的平方;
(2)求出A(0,4)关于直线l:x-2y+4=0的对称点,即可求出||PB|-|PA||的最大值.
(2)求出A(0,4)关于直线l:x-2y+4=0的对称点,即可求出||PB|-|PA||的最大值.
解答:
解:(1)∵点P(m,n)在直线l上有移动,
∴m2+n2的最小值为原点到直线距离的平方,即(
)2=
;
(2)设A(0,4)关于直线l:x-2y+4=0的对称点为(a,b),则
,∴a=1.6,b=0.8,
∴||PB|-|PA||的最大值为
=6.
∴m2+n2的最小值为原点到直线距离的平方,即(
| 4 | ||
|
| 16 |
| 5 |
(2)设A(0,4)关于直线l:x-2y+4=0的对称点为(a,b),则
|
∴||PB|-|PA||的最大值为
| (-2-1.6)2+(-4-0.8)2 |
点评:本题考查两点间距离公式的应用,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
已知双曲线的方程为
-
=1,点A,B在双曲线的右支上,线段AB经过双曲线的右焦点F2,|AB|=m,F1为另一焦点,则△ABF1的周长为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、2a+2m | B、a+m |
| C、4a+2m | D、2a+4m |
已知幂函数y=f(x)图象经过点(4,
),则f(3)=( )
| 1 |
| 2 |
| A、3 | ||||
B、
| ||||
C、
| ||||
D、
|
函数y=log2x,x∈(0,16)的值域是( )
| A、(-∞,-4) |
| B、(-∞,4] |
| C、[-4,+∞) |
| D、[4,+∞) |
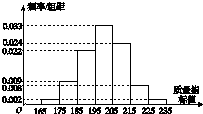 从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得到如图所示的频率分布直方图.
从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得到如图所示的频率分布直方图.