题目内容
8.三棱锥D-ABC中,AB=CD=$\sqrt{6}$,其余四条棱均为2,则三棱锥D-ABC的外接球的表面积为7π.分析 分别取AB,CD的中点E,F,连接相应的线段,由条件可知,球心G在EF上,可以证明G为EF中点,
求出球的半径,再求球的表面积.
解答 解:分别取AB,CD的中点E,F,
连接相应的线段CE,ED,EF,
由条件,AB=CD=$\sqrt{6}$,
BC=AC=AD=BD=2,
可知△ABC与△ADB,
都是等腰三角形,
AB⊥平面ECD,∴AB⊥EF,
同理CD⊥EF,
∴EF是AB与CD的公垂线,
球心G在EF上,
可以证明G为EF中点,(△AGB≌△CGD)
DE=$\sqrt{{2}^{2}{-(\frac{\sqrt{6}}{2})}^{2}}$=$\frac{\sqrt{10}}{2}$,DF=$\frac{\sqrt{6}}{2}$,EF=$\sqrt{{(\frac{\sqrt{10}}{2})}^{2}{-(\frac{\sqrt{6}}{2})}^{2}}$=1,
∴GF=$\frac{1}{2}$,
球半径DG=$\sqrt{{(\frac{1}{2})}^{2}{+(\frac{\sqrt{6}}{2})}^{2}}$=$\frac{\sqrt{7}}{2}$,
∴外接球的表面积为4π×DG2=7π.
故答案为:7π.
点评 本题考查了球的内接几何体以及球的表面积问题,也考查空间想象能力与计算能力.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
19.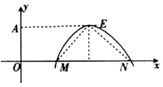 已知奇函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,点M的坐标为(1,0)且△MNE为等腰直角三角形,当A取最大值时,f($\frac{1}{3}$)等于( )
已知奇函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,点M的坐标为(1,0)且△MNE为等腰直角三角形,当A取最大值时,f($\frac{1}{3}$)等于( )
 已知奇函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,点M的坐标为(1,0)且△MNE为等腰直角三角形,当A取最大值时,f($\frac{1}{3}$)等于( )
已知奇函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,点M的坐标为(1,0)且△MNE为等腰直角三角形,当A取最大值时,f($\frac{1}{3}$)等于( )| A. | -$\frac{\sqrt{3}}{4}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -1 |
16.已知向量$\overrightarrow a=(cosθ,sinθ)$,向量$\overrightarrow{b}$=($\sqrt{3}$,1),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则tanθ的值是( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
13.某象棋俱乐部有队员5人,其中女队员2人,现随机选派2人参加象棋比赛,则选出的2人中恰有1人是女队员的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{3}$ |
6.设P:2<x<4,Q:lnx<e,则P是Q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |