题目内容
已知:由五个直角边为
的等腰直角三角形拼成如图所示的平面凹五边形ACDEF,沿AD折起,使平面ADEF⊥平面ACD.
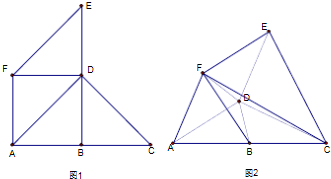
(1)求证:FB⊥AD;
(2)求二面角C-EF-D的正切值.
| 2 |

(1)求证:FB⊥AD;
(2)求二面角C-EF-D的正切值.
考点:用空间向量求平面间的夹角,直线与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(1)作FO⊥AD于O,连结OB,由已知得O为AD中点,BO⊥AD,从而AD⊥平面FOB,由此能证明FB⊥AD.
(2)由已知得∠ADC=90°,CD⊥AD,CD⊥平面ADEF,作DM⊥EF,连结MC,则∠DMC是二面角C-EF-D的平面角,
由此能求出二面角C-EF-D的正切值.
(2)由已知得∠ADC=90°,CD⊥AD,CD⊥平面ADEF,作DM⊥EF,连结MC,则∠DMC是二面角C-EF-D的平面角,
由此能求出二面角C-EF-D的正切值.
解答:
(1)证明:作FO⊥AD于O,连结OB,
∵等腰直角△AFD,∴O为AD中点,
∴等腰直角△ABD,∴BO⊥AD,
∵FO∩BO=O,∴AD⊥平面FOB,
∴FB⊥AD.
(2)解:∵等腰直角△ADB和等腰直角△CDB,
∴∠ADC=90°,∴CD⊥AD,
又∵平面ADEF⊥平面ACD,平面ADEF∩平面ACD=AD,
∴CD⊥平面ADEF,作DM⊥EF,连结MC,
∠DMC是二面角C-EF-D的平面角,
在Rt△MDC中,∠MDC=90°,MD=1,DC=2,
∴tan∠DMC=2,
∴二面角C-EF-D的正切值为2.

∵等腰直角△AFD,∴O为AD中点,
∴等腰直角△ABD,∴BO⊥AD,
∵FO∩BO=O,∴AD⊥平面FOB,
∴FB⊥AD.
(2)解:∵等腰直角△ADB和等腰直角△CDB,
∴∠ADC=90°,∴CD⊥AD,
又∵平面ADEF⊥平面ACD,平面ADEF∩平面ACD=AD,
∴CD⊥平面ADEF,作DM⊥EF,连结MC,
∠DMC是二面角C-EF-D的平面角,
在Rt△MDC中,∠MDC=90°,MD=1,DC=2,
∴tan∠DMC=2,
∴二面角C-EF-D的正切值为2.
点评:本题考查异面直线垂直的证明,考查二面角的正切值的求法,是中档题,解题时要认真审题,注意空思维能力的培养.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
双曲线
-
=1的左右焦点分别为F1,F2,点P为该双曲线在第一像限的点,△PF1F2的面积为1,且tan∠PF1F2=0.5,tan∠PF2F1=-2,则该双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、3x2-
| ||||
D、
|