题目内容
7.若角α=600°的终边上有一点(a,-2),则a的值是( )| A. | $-\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $±\frac{{2\sqrt{3}}}{3}$ | D. | $2\sqrt{3}$ |
分析 根据α的终边在第三象限,利用三角函数的定义求出a的值.
解答 解:角α=600°=720°-120°
∴α的终边在第三象限内,
α终边上有一点(a,-2),
∴a<0;
又cosα=$\frac{a}{\sqrt{{a}^{2}+4}}$=-$\frac{1}{2}$,
∴a=±$\frac{2\sqrt{3}}{3}$,
∴a的值是-$\frac{2\sqrt{3}}{3}$.
故选:A.
点评 本题考查了三角函数的定义与应用问题,是基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
2.在△ABC中,a,b,c分别是内角A,B,C的对边,若A=$\frac{2π}{3}$,b=$\sqrt{2}$,△ABC的面积为$\sqrt{3}$,则a的值为( ) )
| A. | $\sqrt{6}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{14}$ |
19.设函数f(x)在R上存在导函数f′(x),?x∈R,都有f(x)+f(-x)=x2,在x>0时,f′(x)<x,若f(4-m)-f(m)≥8-4m,则实数m的取值范围为( )
| A. | [-2,2] | B. | [2,+∞) | C. | [0,+∞) | D. | (-∞,-2]∪[2,+∞) |
17.在区间(0,2)内随机取出两个数x,y,则1,x,y能作为三角形三条边的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{7}{8}$ |
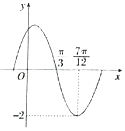 函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,则下列结论:①将f(x)的图象向左平移$\frac{π}{6}$个单位,所得到的函数是偶函数:②f(0)=1;③最小正周期为π;④$f(\frac{12π}{11})<f(\frac{14π}{13})$;⑤$f(x)=-f(\frac{5π}{3}-x)$.其中正确的结论有( )
函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,则下列结论:①将f(x)的图象向左平移$\frac{π}{6}$个单位,所得到的函数是偶函数:②f(0)=1;③最小正周期为π;④$f(\frac{12π}{11})<f(\frac{14π}{13})$;⑤$f(x)=-f(\frac{5π}{3}-x)$.其中正确的结论有( )