题目内容
已知函数f(x)=loga(2x+1)-loga(1-2x).
(1)判断函数f(x)的奇偶性,并给予证明;
(2)若函数y=f(x)与y=m-loga(2-4x)的图象有且仅有一个公共点,求实数m的取值范围.
(1)判断函数f(x)的奇偶性,并给予证明;
(2)若函数y=f(x)与y=m-loga(2-4x)的图象有且仅有一个公共点,求实数m的取值范围.
考点:函数奇偶性的判断,对数的运算性质
专题:函数的性质及应用
分析:(1)首先求出定义域,然后利用定义判断奇偶性;
(2)函数y=f(x)与y=m-loga(2-4x)的图象有且仅有一个公共点?方程loga
=m-loga(2-4x)
在区间x∈(-
,
)上有且仅有一个实数解,讨论a的范围,利用对数函数的单调性求m 范围.
(2)函数y=f(x)与y=m-loga(2-4x)的图象有且仅有一个公共点?方程loga
| 2x+1 |
| 1-2x |
在区间x∈(-
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)f(x)的定义域为(-
,
),关于原点对称,
f(x)+f(-x)=loga
+loga
=loga1=0,所以f(-x)=-f(x),
所以f(x)是奇函数…(5分)
(2)函数y=f(x)与y=m-loga(2-4x)的图象有且仅有一个公共点?方程loga
=m-loga(2-4x)
在区间x∈(-
,
)上有且仅有一个实数解,
m=loga
+loga2(1-2x)=loga(4x+2)…(7分)
因为x∈(-
,
),所以0<4x+2<4
所以loga(4x+2)∈(-∞,loga4)或(loga4,+∞)
∴当a>1时,m∈(-∞,loga4),
当0<a<1时,m∈(loga4,+∞)…(12分)
| 1 |
| 2 |
| 1 |
| 2 |
f(x)+f(-x)=loga
| 2x+1 |
| 1-2x |
| -2x+1 |
| 1+2x |
所以f(x)是奇函数…(5分)
(2)函数y=f(x)与y=m-loga(2-4x)的图象有且仅有一个公共点?方程loga
| 2x+1 |
| 1-2x |
在区间x∈(-
| 1 |
| 2 |
| 1 |
| 2 |
m=loga
| 2x+1 |
| 1-2x |
因为x∈(-
| 1 |
| 2 |
| 1 |
| 2 |
所以loga(4x+2)∈(-∞,loga4)或(loga4,+∞)
∴当a>1时,m∈(-∞,loga4),
当0<a<1时,m∈(loga4,+∞)…(12分)
点评:本题考查了函数奇偶性的判断以及对数函数单调性的运用,属于中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
已知a,b,c是实数,则下列结论中一定正确的是( )
| A、若a>b,则ac>bc |
| B、若a>b,则a-c<b-c |
| C、若ac>bc,则a>b |
| D、若a>|b|,则a>b |
与圆x2+(y-2)2=2相切,且在两坐标轴上截距相等的直线有( )
| A、6条 | B、4条 | C、3条 | D、2条 |
 如图,在正方体ABCD-A1B1C1D1中,线段AD1、B1C所在直线的位置关系是( )
如图,在正方体ABCD-A1B1C1D1中,线段AD1、B1C所在直线的位置关系是( )| A、平行 | B、相交且垂直 |
| C、异面但不垂直 | D、异面且垂直 |
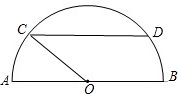 如图是一个半圆形湖面景点的示意图,已知AB为直径,且AB=2km,O为圆心,C为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥AB,现在准备从A经过C到D建造一条观光路线,其中A到C是圆弧
如图是一个半圆形湖面景点的示意图,已知AB为直径,且AB=2km,O为圆心,C为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥AB,现在准备从A经过C到D建造一条观光路线,其中A到C是圆弧
