题目内容
与圆x2+（y-2）2=2相切，且在两坐标轴上截距相等的直线有（ ）
| A、6条 | B、4条 | C、3条 | D、2条 |
考点：圆的切线方程
专题：直线与圆
分析：可设两坐标轴上截距相等（在坐标轴上截距不为0）的直线方程为x+y=a，与圆的方程x2+（y-2）2=4联立，利用△=0即可求得a的值，从而可求得直线方程；另外需要考虑坐标轴上截距都为0的情况．
解答：
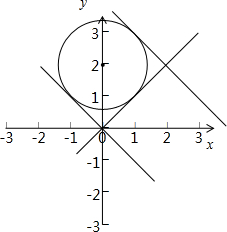解：设两坐标轴上截距相等（在坐标轴上截距不为0）的直线l方程为x+y=a，
则由题意得：
，消去y得：2x2+（4-2a）x+a2-4a+2=0，
∵l与圆x2+（y-2）2=2相切，
∴△=（4-2a）2-4×2（a2-4a+2）=0，
解得a=0或a=4，
∴l的方程为：x+y=0或x+y=0；
当坐标轴上截距都为0时，由图可知y=x与该圆相切；
共有3条满足题意的直线．
故选：C．
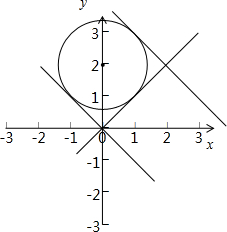解：设两坐标轴上截距相等（在坐标轴上截距不为0）的直线l方程为x+y=a，则由题意得：
|
∵l与圆x2+（y-2）2=2相切，
∴△=（4-2a）2-4×2（a2-4a+2）=0，
解得a=0或a=4，
∴l的方程为：x+y=0或x+y=0；
当坐标轴上截距都为0时，由图可知y=x与该圆相切；
共有3条满足题意的直线．
故选：C．
点评：本题考查直线与圆的位置关系，易错点在于忽略坐截距都为0时相切的情况，属于中档题．基本知识的考查．
练习册系列答案
一线名师权威作业本系列答案
相关题目
若曲线 y=x2 上P点处的切线平行于 2x-y+1=0，则点P的坐标是（ ）
| A、（ 1，-1） |
| B、（-1，1） |
| C、（ 1，1） |
| D、（-1，-1） |
已知函数：f1（x）=ln
，f2（x）=lg（x+
），f3（x）=（x-1）
，f4（x）=
，
f5（x）=1-
，f6（x）=-xsin（
+x），则为奇函数的有（ ）个．
| 1-x |
| 1+x |
| x2+1 |
|
|
f5（x）=1-
| 2 |
| 2x+1 |
| π |
| 2 |
| A、5 | B、4 | C、3 | D、2 |
直线3x-4y-9=0与圆x2+y2=4的位置关系是（ ）
| A、相交且过圆心 | B、相切 |
| C、相离 | D、相交但不过圆心 |