题目内容
14.已知抛物线C:y2=8x与点M(-2,2),过C的焦点且斜率为k的直线与C交于A,B两点,若$\sqrt{2}$$\overrightarrow{MA}$•$\overrightarrow{MB}$=0,则k=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
分析 斜率k存在,设直线AB为y=k(x-2),代入抛物线方程,利用(x1+2,y1-2)•(x2+2,y2-2)=0,即可求出k的值.
解答 解:由抛物线C:y2=8x得焦点(2,0),
由题意可知:斜率k存在,设直线AB为y=k(x-2),
代入抛物线方程,得到k2x2-(4k2+8)x+4k2=0,△>0,
设A(x1,y1),B(x2,y2).
∴x1+x2=4+$\frac{8}{{k}^{2}}$,x1x2=4.
∴y1+y2=$\frac{8}{k}$,y1y2=-16
又$\sqrt{2}$$\overrightarrow{MA}$•$\overrightarrow{MB}$=0,
∴(x1+2,y1-2)•(x2+2,y2-2)=$\frac{16}{{k}^{2}}$-$\frac{16}{k}$+4=0
∴k=2.
故选D.
点评 本题考查直线与抛物线的位置关系,考查向量的数量积公式,考查学生的计算能力,属于中档题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
5.已知椭圆方程为$\frac{x^2}{9}+\frac{y^2}{4}=1$的左、右焦点分别为F1,F2,过左焦点F1的直线交椭圆于A,B两点,则△ABF2的周长为( )
| A. | 12 | B. | 9 | C. | 6 | D. | 4 |
3.命题p:方程$\frac{x^2}{m-5}-\frac{y^2}{m+3}=1$表示双曲线的充要条件是-3<m<5;
命题q:存在x0∈R,使得sinx0-cosx0=2,则( )
命题q:存在x0∈R,使得sinx0-cosx0=2,则( )
| A. | 命题“p或q”是假命题 | B. | 命题“p且q”是真命题 | ||
| C. | 命题“非q”是假命题 | D. | 命题“p且‘非q’”是真命题 |
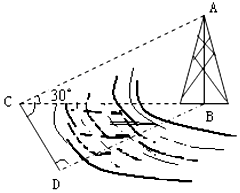 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与∠BCD=75°,∠BDC=60°,CD=20mD.现测得,并在点C测得塔顶A的仰角为30°,求塔高AB.
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与∠BCD=75°,∠BDC=60°,CD=20mD.现测得,并在点C测得塔顶A的仰角为30°,求塔高AB.