已知椭圆方程为$\frac{x^2}{9}+\frac{y^2}{4}=1$的左.右焦点分别为F1.F2.过左焦点F1的直线交椭圆于A.B两点.则△ABF2的周长为( )A．12B．9C．6D．4 题目和参考答案——青夏教育精英家教网—

题目内容

5．已知椭圆方程为$\frac{x^2}{9}+\frac{y^2}{4}=1$的左、右焦点分别为F₁，F₂，过左焦点F₁的直线交椭圆于A，B两点，则△ABF₂的周长为（　　）

A．

B．

C．

D．

分析由椭圆方程为$\frac{x^2}{9}+\frac{y^2}{4}=1$焦点在x轴上，a=3，根据椭圆的定义可知：椭圆的定义可知：|AF₁|+|AF₂|=2a=6，|BF₁|+|BF₂|=2a=6，则△ABF₂的周长（|AF₁|+|AF₂|）+（|BF₁|+|BF₂|）=4a=12．

解答解：椭圆方程为$\frac{x^2}{9}+\frac{y^2}{4}=1$焦点在x轴上，a=3，b=2，c=$\sqrt{5}$，
由椭圆的定义可知：|AF₁|+|AF₂|=2a=6，|BF₁|+|BF₂|=2a=6，
则△ABF₂的周长（|AF₁|+|AF₂|）+（|BF₁|+|BF₂|）=2a+2a=4a=12，
∴△ABF₂的周长12，
故选A．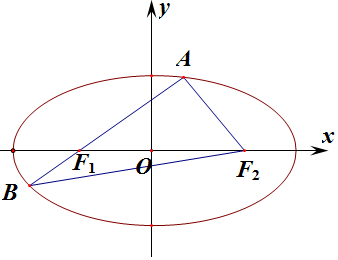

点评本题考查椭圆的标准方程，考查椭圆的定义及焦点三角形的性质，考查数形结合思想，属于基础题．

练习册系列答案

南大励学小学生英语四合一阅读组合训练系列答案

16．已知函数f（x）=x³-ax²+b，曲线y=f（x）在点（2，4）处的切线方程为4x-y-4=0．
（Ⅰ）求a，b 的值；
（Ⅱ）求函数f（x）在[-1，3]上的最大值．

13．如图中程序运行后输出的结果为（　　）

20．已知函数f（x）=$\frac{2x}{{{x^2}+1}}$，则下列说法正确的是（　　）

	A．	函数f（x）在（0，+∞）上有最小值		B．	函数f（x）在（0，+∞）上没有最大值
	C．	函数f（x）在R上没有极小值		D．	函数f（x）在R上有极大值

10．△ABC的内角A，B，C的对边分别为a，b，c，已知2cosC（acosB+bcosA）=c．
（1）求角C；
（2）若$c=\sqrt{7}$，△ABC的面积为$\frac{{3\sqrt{3}}}{2}$，求a+b的值．

17．已知等比数列{a_n}的首项a₁=1，公比为q，试就q的不同取值情况，讨论二元一次方程组$\left\{\begin{array}{l}{a_1}x+{a_3}y=3\\{a_2}x+{a_4}y=-2\end{array}\right.$何时无解，何时有无穷多解？

14．已知抛物线C：y²=8x与点M（-2，2），过C的焦点且斜率为k的直线与C交于A，B两点，若$\sqrt{2}$$\overrightarrow{MA}$•$\overrightarrow{MB}$=0，则k=（　　）

15．已知{a_n}是首项为1的等差数列，{b_n}是首项为2且各项均为正数的等比数列，且满足a₂+a₃=b₃，5+b₂=3a₂．
（1）求{a_n}和{b_n}的通项公式；
（2）设c_n=（-1）ⁿa_na_n+1，求数列{c_n}的前2n项和T_2n；
（3）设{b_n}的前n项和为S_n，是否存在正整数n，t，使得$\frac{{S}_{n}-t{b}_{n}}{{S}_{n+1}-t{b}_{n+1}}$＜$\frac{1}{16}$成立？若存在，求出正整数n，t；若不存在，请说明理由．

试题分类