题目内容
9.在△ABC中,已知A=$\frac{π}{3}$.(1)若B=$\frac{5π}{12}$,c=$\sqrt{6}$,求a;
(2)若a=$\sqrt{7}$,c=2,求边b.
分析 (1)由已知利用三角形内角和定理可求C的值,进而利用正弦定理可求a的值.
(2)由已知利用余弦定理即可解得b的值.
解答 (本题满分为12分)
解:(1)∵A=$\frac{π}{3}$.B=$\frac{5π}{12}$,
∴由题意可得:C=π-$\frac{π}{3}$-$\frac{5π}{12}$=$\frac{π}{4}$,…(2分)
∵c=$\sqrt{6}$,
∴由正弦定理$\frac{a}{sina}=\frac{c}{sinC}$,可得:a=$\frac{csinA}{sinC}=\frac{\sqrt{6}×\frac{\sqrt{3}}{2}}{\frac{\sqrt{2}}{2}}$=3,…(6分)
(2)∵a=$\sqrt{7}$,c=2,A=$\frac{π}{3}$.
∴由余弦定理,a2=b2+c2-2bccosA,…(8分)
可得:($\sqrt{7}$)2=b2+22-2b×$2cos\frac{π}{3}$,…(10分)
∴解得:b=-1(舍去)或b=3.…(12分)
点评 本题主要考查了三角形内角和定理,正弦定理,余弦定理在解三角形中的综合应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
14.已知抛物线C:y2=8x与点M(-2,2),过C的焦点且斜率为k的直线与C交于A,B两点,若$\sqrt{2}$$\overrightarrow{MA}$•$\overrightarrow{MB}$=0,则k=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
1.命题“存在x0≥0,${2}^{{x}_{0}}$≤0”的否定是( )
| A. | 不存在x0≥0,${2}^{{x}_{0}}$>0 | B. | 存在x0≥0,${2}^{{x}_{0}}$≥0 | ||
| C. | 对任意的x0≥0,2x≤0 | D. | 对任意的x0≥0,2x>0 |
18.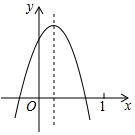 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①b<0,c>0;②a+b+c<0;③方程的两根之和大于0;④a-b+c<0,其中正确的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①b<0,c>0;②a+b+c<0;③方程的两根之和大于0;④a-b+c<0,其中正确的个数是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①b<0,c>0;②a+b+c<0;③方程的两根之和大于0;④a-b+c<0,其中正确的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①b<0,c>0;②a+b+c<0;③方程的两根之和大于0;④a-b+c<0,其中正确的个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
19.下列命题中,真命题是( )
| A. | 所有的素数是奇数 | B. | ?x∈R,x+$\frac{1}{x}$≥2 | ||
| C. | ?x∈R,x2-2x-3=0 | D. | 存在两个相交平面垂直于同一直线 |