题目内容
6.某次文艺晚会上共演出8个节目,其中2个唱歌、3个舞蹈、3个曲艺节目,求分别满足下列条件的排节目单的方法种数:(1)一个唱歌节目开头,另一个压台;
(2)两个唱歌节目不相邻;
(3)两个唱歌节目相邻且3个舞蹈节目不相邻.
分析 (1)先排歌曲节目,再排其他节目,利用乘法原理,即可得出结论;
(2)先排3个舞蹈,3个曲艺节目,再利用插空法排唱歌,即可得到结论;
(3)两个唱歌节目相邻,用捆绑法,3个舞蹈节目不相邻,利用插空法,即可得到结论.
解答 解:(1)先排歌曲节目有A22种排法,再排其他节目有A66种排法,所以共有A22A66=1440种排法.
(2)先排3个舞蹈节目,3个曲艺节目,有A66种排法,再从其中7个空(包括两端)中选2个排歌曲节目,有A72种插入方法,所以共有A66A72=30240种排法.
(3)两个唱歌节目相邻,用捆绑法,3个舞蹈节目不相邻,利用插空法,共有A44A53A22=2880种.
点评 本题考查排列组合知识,考查学生利用数学知识解决实际问题的能力,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
14.已知抛物线C:y2=8x与点M(-2,2),过C的焦点且斜率为k的直线与C交于A,B两点,若$\sqrt{2}$$\overrightarrow{MA}$•$\overrightarrow{MB}$=0,则k=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
11.函数$f(x)=\frac{{3{x^2}-8lnx}}{2lnx}$在[2,4]上的最大值为( )
| A. | $\frac{6-4ln2}{ln2}$ | B. | $\frac{6}{ln2}+4$ | C. | $\frac{12}{ln2}-4$ | D. | 3e-4 |
1.命题“存在x0≥0,${2}^{{x}_{0}}$≤0”的否定是( )
| A. | 不存在x0≥0,${2}^{{x}_{0}}$>0 | B. | 存在x0≥0,${2}^{{x}_{0}}$≥0 | ||
| C. | 对任意的x0≥0,2x≤0 | D. | 对任意的x0≥0,2x>0 |
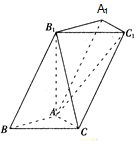 已知三棱柱ABC-A1B1C1中,AA1=B1C=2AB=2AC=2,∠BAC=90°,∠BAA1=120°.
已知三棱柱ABC-A1B1C1中,AA1=B1C=2AB=2AC=2,∠BAC=90°,∠BAA1=120°.