题目内容
曲线y=lnx-1在x=1处的切线方程为 ．
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：切线斜率k=y′|x=1=1，再求出切点的坐标，利用点斜式即可写出切线方程．
解答：
解：因为y=lnx-1，
所以y′=
，则切线斜率k=y′|x=1=1，
因为x=1时，y=-1，
所以在x=1处的切线方程为：y+1=x-1，即x-y-2=0．
故答案为：x-y-2=0．
所以y′=
| 1 |
| x |
因为x=1时，y=-1，
所以在x=1处的切线方程为：y+1=x-1，即x-y-2=0．
故答案为：x-y-2=0．
点评：本题考查利用导数研究曲线上某点切线方程，考查直线方程的求法，考查导数的几何意义，属基础题．
练习册系列答案
科学实验活动册系列答案
相关题目
从高三年级随机抽取100名学生，将他们的某次考试数学成绩绘制成频率分布直方图．由图中数据可知成绩在[130，140）内的学生人数为（ ）| A、20 | B、25 | C、30 | D、35 |
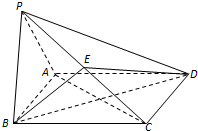如图，在四棱锥P-ABCD中，底面ABCD为矩形，平面PAB⊥平面ABCD，PA⊥PB，BP=BC，E为PC的中点．
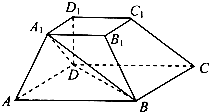如图，在四棱台ABCD-A1B1C1D1中，底面ABCD是平行四边形，DD1⊥平面ABCD，AB=2AD，AD=A1B1，∠BAD=60°．