题目内容
某高中有高一、高二、高三共三个学年,根据学生的综合测评分数分为学优生和非学优生两类,某月三个学年的学优生和非学优生的人数如表所示(单位:人),若用分层抽样的方法从三个学年中抽取50人,则高一共有10人.
(1)求z的值;
(2)用随机抽样的方法从高二学年学优生中抽取8人,经检测他们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8人的得分看作一个总体,从中任取一个分数a.记这8人的得分的平均数为
,定义事件E={|a-
|≤0.5,且f(x)=ax2-ax+2.31没有零点},求事件E发生的概率.
| 高一学年 | 高二学年 | 高三学年 | |
| 学优生 | 100 | 150 | z |
| 非学优生 | 300 | 450 | 600 |
(2)用随机抽样的方法从高二学年学优生中抽取8人,经检测他们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8人的得分看作一个总体,从中任取一个分数a.记这8人的得分的平均数为
. |
| x |
. |
| x |
考点:古典概型及其概率计算公式,分层抽样方法,众数、中位数、平均数
专题:概率与统计
分析:第(1)问涉及分层抽样知识,第(2)问涉及古典概型与平均数的计算.
解答:
解:(1)根据分层抽样的特征,有
=
,
解得z=400.
(2)由题意,
=9.
由|a-
|≤0.5,得8.5≤a≤9.5.
由f(x)=ax2-ax+2.31没有零点,得0<a<9.24.
所以,符合上述两个条件的a=8.6,9.2,8.7,9.0,共4个值,
故所求概率为P=
=
.
| 400 |
| 1600+z |
| 10 |
| 50 |
解得z=400.
(2)由题意,
. |
| x |
由|a-
. |
| x |
由f(x)=ax2-ax+2.31没有零点,得0<a<9.24.
所以,符合上述两个条件的a=8.6,9.2,8.7,9.0,共4个值,
故所求概率为P=
| 4 |
| 8 |
| 1 |
| 2 |
点评:本题考查了抽样方法与古典概型知识,属基础题.掌握了分层抽样的特征与古典概型概率计算公式即可正确求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知α=2,则点P(sinα,tanα)所在的象限是( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
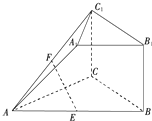 如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,CA=CB,A1B1∥AB,AB=2A1B1,E,F分别是AB,AC1的中点.
如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,CA=CB,A1B1∥AB,AB=2A1B1,E,F分别是AB,AC1的中点.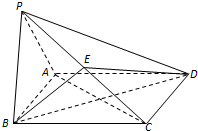 如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PC的中点.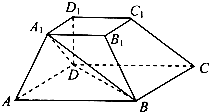 如图,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=2AD,AD=A1B1,∠BAD=60°.
如图,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=2AD,AD=A1B1,∠BAD=60°.