题目内容

某几何体的三视图如图所示，则该几何体的体积为
 
．
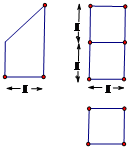
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：几何体是一个单位正方体与半个单位正方体的组合体，由此可得几何体的体积．
解答： 解：由三视图知：几何体是一个单位正方体与半个单位正方体的组合体，
∴几何体的体积V=1+
1
2
=
3
2
．
故答案为：
3
2
．
点评：本题考查了由三视图求几何体的体积，根据三视图判断几何体的形状是关键．
练习册系列答案
相关题目
如图是抛物线形拱桥，当水面在l时，拱顶离水面2米，水面宽4米，水位上升1米后，水面宽
 
米．
关于函数f（x）=cos（2x-
π
3
）+cos（2x+
π
6
）有下列命题：
①y=f（x）的最大值为
2
；
②y=f（x）的一条对称轴方程是x=
π
24
；
③y=f（x）在区间（
π
24
，
13π
24
）上单调递减；
④将函数y=
2
cos2x的图象向左平移
5π
24
个单位后，与已知函数的图象重合．
其中正确命题的序号是
 
．（注：把你认为正确的命题的序号都填上）
有下列4个命题：
①函数f（x）=lg（
cosx-1
+
1-cosx
+1）既是奇函数又是偶函数；
②函数f（x）=4sin（2x+
π
3
）（x∈R），图象关于点（-
π
6
，0）对称，也关于直线x=
π
6
对称；
③若f（x）是R上周期为5的奇函数，且满足f（1）=1，f（2）=2，则f（3）-f（4）=-1；
④已知
sinα
sinβ
=p，
cosα
cosβ
=q，且p≠±1，q≠0，则tanαtanβ=
p(q2-1)
q(p2-1)
；
其中假命题的序号是
 
．
函数f（x）=3x的导数是
 
．
在△ABC中，a=
3
，c=1，B=60°，则△ABC的面积为
 
．
圆C：（x-1）2+（y+2）2=4关于直线x+y=1对称的圆的方程为
 
．
公比为2的等比数列{an}的各项都是正数，且a3a11=16，则log2a1=（　　）
A、4B、-4C、2D、-2
函数f（x）=ln|x|（x≠0），则函数y=
1
f′(x)
+4f′（x）在（-∞，0）上的最大值是（　　）
A、4B、-4C、2D、-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网