题目内容
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0．-
＜φ＜
）的图象与x轴交点为（-
，0），相邻最高点坐标为（
，1）．
（1）求函数y=f（x）的表达式；
（2）若y=g（x）的图象与y=f（x）的图象关于点（
，0）成中心对称，求y=g（x）的解析式及单调增区间．
（3）求函数h（x）=log
f（x）的单调增区间．
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
| π |
| 12 |
（1）求函数y=f（x）的表达式；
（2）若y=g（x）的图象与y=f（x）的图象关于点（
| π |
| 12 |
（3）求函数h（x）=log
| 1 |
| 2 |
考点：函数y=Asin（ωx+φ）的图象变换
专题：函数的性质及应用,三角函数的图像与性质
分析：（1）根据题意，求出A、ω与φ的值，即得f（x）的解析式；
（2）求出与y=f（x）的图象关于点（
，0）成中心对称的函数g（x），再求出它的单调增区间；
（3）求出h（x）的定义域，再根据复合函数的单调性，求出h（x）的单调增区间．
（2）求出与y=f（x）的图象关于点（
| π |
| 12 |
（3）求出h（x）的定义域，再根据复合函数的单调性，求出h（x）的单调增区间．
解答：
解：（1）根据题意，A=1，
ω+φ=
，
又（-
）ω+φ=0；
解得ω=2，φ=
，
∴f（x）=sin（2x+
）；
（2）∵与y=f（x）的图象关于点（
，0）成中心对称的函数是
-y=f（-（x-2×
）），
即-y=sin[-2（x-
）+
]，
∴y=sin（2x-
）；
即g（x）=sin（2x-
）；
令-
+2kπ≤2x-
≤
+2kπ，k∈Z，
∴
+2kπ≤2x≤
+2kπ，k∈Z，
即
+kπ≤x≤
+kπ，k∈Z；
∴g（x）的单调增区间是[
+kπ，
+kπ]，k∈Z；
（3）∵h（x）=log
f（x）=log
sin（2x+
），
∴sin（2x+
）＞0，且sin（2x+
）是减函数；
∴2kπ+
≤2x+
＜π+2kπ，k∈Z；
即
+2kπ≤2x＜
+2kπ，k∈Z，
∴
+kπ≤x＜
+kπ，k∈Z；
∴h（x）的单调增区间是[
+kπ，
+kπ），k∈Z．
| π |
| 12 |
| π |
| 2 |
又（-
| π |
| 6 |
解得ω=2，φ=
| π |
| 3 |
∴f（x）=sin（2x+
| π |
| 3 |
（2）∵与y=f（x）的图象关于点（
| π |
| 12 |
-y=f（-（x-2×
| π |
| 12 |
即-y=sin[-2（x-
| π |
| 6 |
| π |
| 3 |
∴y=sin（2x-
| 2π |
| 3 |
即g（x）=sin（2x-
| 2π |
| 3 |
令-
| π |
| 2 |
| 2π |
| 3 |
| π |
| 2 |
∴
| π |
| 6 |
| 7π |
| 6 |
即
| π |
| 12 |
| 7π |
| 12 |
∴g（x）的单调增区间是[
| π |
| 12 |
| 7π |
| 12 |
（3）∵h（x）=log
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
∴sin（2x+
| π |
| 3 |
| π |
| 2 |
∴2kπ+
| π |
| 2 |
| π |
| 3 |
即
| π |
| 6 |
| 2π |
| 3 |
∴
| π |
| 12 |
| π |
| 3 |
∴h（x）的单调增区间是[
| π |
| 12 |
| π |
| 3 |
点评：本题考查了三角函数的图象与性质的应用问题，也考查了复合函数的单调性问题，函数图象的对称问题，
是综合题目．
是综合题目．
练习册系列答案
相关题目
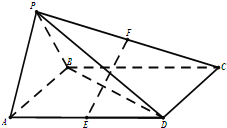四棱锥P-ABCD底面是平行四边形，平面PAB⊥平面ABCD，PA=PB=AB=