题目内容
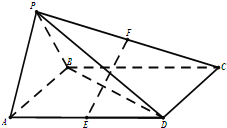 四棱锥P-ABCD底面是平行四边形,平面PAB⊥平面ABCD,PA=PB=AB=
四棱锥P-ABCD底面是平行四边形,平面PAB⊥平面ABCD,PA=PB=AB=| 1 |
| 2 |
(Ⅰ)求证:EF∥平面PAB
(Ⅱ)求三棱锥VP-ABD.
考点:直线与平面平行的判定
专题:计算题,作图题,证明题,空间位置关系与距离
分析:(1)取PB中点G,连接AG,FG,由线线平行证明线面平行,(2)在平面PAB中,作PH⊥AB于点H.求底面面积和体高,可得体积.
解答:
解:(1)证明:取PB中点G,连接AG,FG,
又∵F为PC的中点,
∴GF是△PBC的中位线,
即GF
BC,
∵四边形ABCD底面是平行四边形,E分别为AB的中点,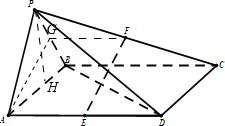
∴AE
BC,
∴GF
AE,
即四边形AEFG是平行四边形,
∴EF∥AG,又∵AG?平面PAB,
∴EF∥平面PAB.
(2)在平面PAB中,作PH⊥AB于点H.
∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,PH?平面PAB,PH⊥AB,
∴PH⊥平面ABCD,
∴PH是三棱锥P-ABD的高,
∵在等边三角形PAB中,PA=PB=AB=1,
∴PH=
,
∵在△ABD中,AB=1,AD=2,∠BAD=600∴S△ABD=
×2×1×sin600=
∴VP-ABD=
S△ABD•PH=
×
×
=
.
又∵F为PC的中点,
∴GF是△PBC的中位线,
即GF
| ||
. |
| 1 |
| 2 |
∵四边形ABCD底面是平行四边形,E分别为AB的中点,

∴AE
| ||
. |
| 1 |
| 2 |
∴GF
| ||
. |
即四边形AEFG是平行四边形,
∴EF∥AG,又∵AG?平面PAB,
∴EF∥平面PAB.
(2)在平面PAB中,作PH⊥AB于点H.
∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,PH?平面PAB,PH⊥AB,
∴PH⊥平面ABCD,
∴PH是三棱锥P-ABD的高,
∵在等边三角形PAB中,PA=PB=AB=1,
∴PH=
| ||
| 2 |
∵在△ABD中,AB=1,AD=2,∠BAD=600∴S△ABD=
| 1 |
| 2 |
| ||
| 2 |
∴VP-ABD=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 4 |
点评:本题考查了辅助线的作法,线线平行证明线面平行的一般方法及体积的求法,属于中档题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 如图,在四面体ABCD中,CB=CD,AD⊥BD,点E,F分别是AB,BD的中点.
如图,在四面体ABCD中,CB=CD,AD⊥BD,点E,F分别是AB,BD的中点.