题目内容
16.已知a,b,c分别是锐角△ABC的三个内角A,B,C的对边,a=1,b=2cosC,sinCcosA-sin($\frac{π}{4}$-B)sin($\frac{π}{4}$+B)=0,则△ABC的内角B的大小为$\frac{π}{6}$.分析 a=1,b=2cosC,利用正弦定理可得:sinB=2sinAcosC.由sinCcosA-sin($\frac{π}{4}$-B)cos($\frac{π}{4}$-B)=0,利用诱导公式可得:sinCcosA-$\frac{1}{2}$sin(2×$\frac{π}{4}$-2B)=0,
利用倍角公式可得:2sinCcosA=1-2sin2B,联立化简即可得出.
解答 解:∵锐角△ABC中,a=1,b=2cosC,∴$\frac{1}{sinA}=\frac{2cosC}{sinB}$,可得sinB=2sinAcosC.
∵sinCcosA-sin($\frac{π}{4}$-B)sin($\frac{π}{4}$+B)=0,sin($\frac{π}{4}$+B)=$cos(\frac{π}{4}-B)$,
∴sinCcosA-sin($\frac{π}{4}$-B)cos($\frac{π}{4}$-B)=0,∴sinCcosA-$\frac{1}{2}$sin(2×$\frac{π}{4}$-2B)=0,
∴sinCcosA-$\frac{1}{2}$cos2B=0,
∴2sinCcosA=1-2sin2B,
∴2sin(A+C)=sinB+1-2sin2B,
∴2sin2B+sinB-1=0,
解得sinB=$\frac{1}{2}$,B∈$(0,\frac{π}{2})$,
∴B=$\frac{π}{6}$.
故答案为:$\frac{π}{6}$.
点评 本题考查了正弦定理、倍角公式、诱导公式、和差化积公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
7.四位男演员与五位女演员(包含女演员甲)排成一排拍照,其中四位男演员互不相邻,且女演员甲不站两侧的排法数为( )
| A. | ${A}_{5}^{5}$${A}_{6}^{4}$-2${A}_{4}^{4}$${A}_{5}^{4}$ | B. | ${A}_{5}^{5}$${A}_{4}^{4}$-${A}_{4}^{4}$${A}_{5}^{4}$ | ||
| C. | ${A}_{6}^{5}$${A}_{5}^{4}$-2${A}_{4}^{4}$${A}_{4}^{4}$ | D. | ${A}_{5}^{5}$${A}_{5}^{4}$-${A}_{4}^{4}$${A}_{4}^{4}$ |
4.若实数b满足:(3+bi)(1+i)-2是纯虚数,则实数b=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |

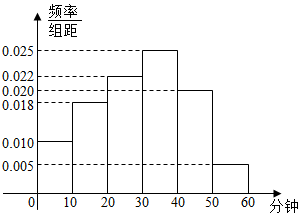 某校为了解本校学生的课后玩电脑游戏时长情况,随机抽取了100名学生进行调查.如图是根据调查结果绘制的学生每天玩电脑游戏的时长的频率分布直方图.
某校为了解本校学生的课后玩电脑游戏时长情况,随机抽取了100名学生进行调查.如图是根据调查结果绘制的学生每天玩电脑游戏的时长的频率分布直方图.