题目内容
1.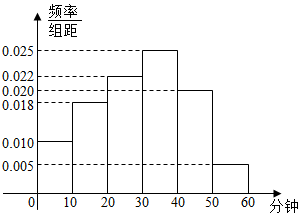 某校为了解本校学生的课后玩电脑游戏时长情况,随机抽取了100名学生进行调查.如图是根据调查结果绘制的学生每天玩电脑游戏的时长的频率分布直方图.
某校为了解本校学生的课后玩电脑游戏时长情况,随机抽取了100名学生进行调查.如图是根据调查结果绘制的学生每天玩电脑游戏的时长的频率分布直方图.(Ⅰ)根据频率分布直方图估计抽取样本的平均数$\overline{x}$和众数m(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)已知样本中玩电脑游戏时长在[50,60]的学生中,男生比女生多1人,现从中选3人进行回访,记选出的男生人数为ξ,求ξ的分布列与期望E(ξ).
分析 (Ⅰ)由频率分布直方图中,[30,40)对应的小矩形最高,能求出m,由频率分布直方图,能求出抽取样本的平均数$\overline{x}$.
(Ⅱ)样本中玩电脑游戏时长在[50,60]的学生为5人,其中男生3人,女生2人,则ξ的可能取值为1,2,3,分别求出相应的概率,由此能求出ξ的分布列和数学期望.
解答 解:(Ⅰ)∵频率分布直方图中,[30,40)对应的小矩形最高,∴m=35,
由频率分布直方图,得:
$\overline x=5×0.1+15×0.18+25×0.22+35×0.25+45×0.2+55×0.05=29.2$.
(Ⅱ)样本中玩电脑游戏时长在[50,60]的学生为0.05×100=5人,
其中男生3人,女生2人,则ξ的可能取值为1,2,3
$P(ξ=1)=\frac{C_3^1C_2^2}{C_5^3}=\frac{3}{10}$,
$P(ξ=2)=\frac{C_3^2C_2^1}{C_5^3}=\frac{6}{10}=\frac{3}{5}$,
$P(ξ=3)=\frac{C_3^3}{C_5^3}=\frac{1}{10}$,
∴ξ的分布列为:
| ξ | 1 | 2 | 3 |
| P(ξ) | $\frac{3}{10}$ | $\frac{3}{5}$ | $\frac{1}{10}$ |
点评 本题考查样本平均数、众数的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识、频率分布直方图的性质的合理运用.

练习册系列答案
相关题目
11.执行如图所示的程序框图,若输入的x,y∈R,则输出t的最大值为( )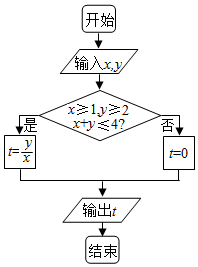

| A. | 1 | B. | 3 | C. | 2 | D. | 0 |
12.若复数z=$\frac{3+2i}{1-i}$(i为虚数单位),则z的共轭复数$\overline{z}$为( )
| A. | $\frac{1}{2}$+$\frac{5}{2}$i | B. | $\frac{1}{2}$-$\frac{5}{2}$i | C. | $\frac{1}{2}$+2i | D. | $\frac{1}{2}$-2i |
9.某次招聘考试中,考生甲在答对第一道题的情况下也答对第二道题的概率为0.8,这两道题均答对的概率为0.5,则考生甲答对第一道题的概率为( )
| A. | $\frac{7}{20}$ | B. | $\frac{1}{20}$ | C. | $\frac{5}{8}$ | D. | $\frac{2}{7}$ |
6.若集合A={-2,-1,0,1,3},集合B={x|x<sin2},则A∩B等于( )
| A. | {-2} | B. | {-2,-1} | C. | {-2,-1,0} | D. | {0,1,3} |
11.口袋中有编号分别为1、2、3的三个大小和形状相同的小球,从中任取2个,则取出的球的最大编号X的均值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |
 某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下:
某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下: