题目内容

11．函数f（x）=$\frac{{x}^{3}}{3}$-sin2x的图象大致是（　　）
A．B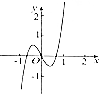．C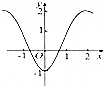．D．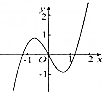

分析 函数的奇偶性和函数值的变化趋势即可判断．

解答 解：因为f（-x）=$\frac{（-x）^{3}}{3}$-sin（-2x）=-f（x），
所以函数f（x）为奇函数，故图象关于原点对称，故排除C，
∵-1≤sin2x≤1，
∴当x→+∞时，f（x）→+∞，故排除A，
但x=1是，f（1）＜$\frac{1}{3}$+sin2＞0，故排除D，
故选：B．

点评 本题考查了函数的图象的识别，关键是掌握函数的奇偶性和函数值的变化趋势，属于基础题．

练习册系列答案
相关题目
1．已知U={x|y=$\sqrt{{{log}_2}x}$}，M={y|y=2x，x≥1}，则∁UM=（　　）
A．[1，2）B．（0，+∞）C．[2，+∞）D．（0，1]
2．已知函数f（x）=（x-k）ex（k∈R）．
（1）若k=0，求函数f（x）的极值；
（2）求函数g（x）在区间[0，1]上的最小值．
19．已知f（x）=ax2+bx+1（a＞0，b∈R）的最小值为-a，f（x）=0的两个实根为x1，x2，P={x|f（x）＜0，x∈R}
（1）求证：|x1-x2|=2；
（2）若g（x）=f（x）+2x在x∈P上存在最小值，求a的取值范围；
（3）若0＜x1＜2，求b的取值范围．
6．已知公差不为零的等差数列{an}满足：a1=3，且a1，a4，a13成等比数列．
（1）求数列{an}的通项公式；
（2）若Sn表示数列{an}的前n项和，求数列{$\frac{1}{{S}_{n}}$}的前n项和Tn．
16．已知a，b，c分别是锐角△ABC的三个内角A，B，C的对边，a=1，b=2cosC，sinCcosA-sin（$\frac{π}{4}$-B）sin（$\frac{π}{4}$+B）=0，则△ABC的内角B的大小为$\frac{π}{6}$．
3．设A市120急救中心与B小区之间开120急救车所用时间为X分钟（单程），所用时间只与道路通畅状况有关，取容量为50的样本进行统计，如表：
X（分钟）25303540
频数6191510
（1）求X的分布列与数学期望；
（2）若A市120急救中心接到来自B小区的急救电话后准备接病人进行救护，若从小区接病人上急救车大约需要5分钟时间，求急救车从急救车中心出发接上病人返回到急救中心不超过75分钟的概率．
20．关于函数f（x）=2sin2x+2$\sqrt{3}$cos2x，下面结论正确的是（　　）
A．在区间$[{\frac{π}{12}，\frac{7π}{12}}]$单调递减B．在区间$[{\frac{π}{12}，\frac{7π}{12}}]$单调递增
C．在区间$[{-\frac{π}{6}，\frac{π}{3}}]$单调递减D．在区间$[{-\frac{π}{6}，\frac{π}{3}}]$单调递增
1．在△ABC中，角A，B，C的对边分别为a，b，c，已知（sinA-sinB）（a+b）=$（\frac{1}{2}a-c）sinC$，则sinB=$\frac{\sqrt{15}}{4}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网