题目内容
已知函数f(x)=
在(0,+∞)上是减函数,那么a的取值范围是 .
|
考点:函数单调性的性质
专题:计算题,函数的性质及应用
分析:要使函数f(x)=
在(0,+∞)上是减函数,则需
解出它们即可得到a的取值范围.
|
|
解答:
解:函数f(x)=
在(0,+∞)上是减函数,
则需
即有
,
解得,0<a≤
,
则a的取值范围是(0,
].
故答案为:(0,
].
|
则需
|
|
解得,0<a≤
| 1 |
| 7 |
则a的取值范围是(0,
| 1 |
| 7 |
故答案为:(0,
| 1 |
| 7 |
点评:本题考查分段函数的单调性,注意各段的单调性以及分界点的情况,考查预算内能力,属于中档题和易错题.

练习册系列答案
相关题目
已知命题p:?x∈R,x-2>0,命题q:?x∈R,
>x,则下列说法中正确的是( )
| x |
| A、命题p∨q是假命题 |
| B、命题p∧q是真命题 |
| C、命题p∨(¬q)是假命题 |
| D、命题p∧(¬q)是真命题 |
已知集合A={x|x<0},B={x|
<2x<4},则A∩B等于( )
| 1 |
| 2 |
| A、{x|-1<x<2} |
| B、{x|-1<x<0} |
| C、{x|x<1} |
| D、{x|-2<x<0} |
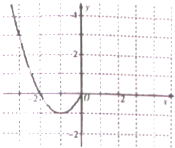 已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)图象是抛物线的一部分(如图所示).
已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)图象是抛物线的一部分(如图所示).