题目内容
20.函数f(x)=1+$\frac{2}{3x}$的图象与y=g(x)的图象关于x轴对称,则g(x)=-1-$\frac{2}{3x}$,函数f(x)与y=h(x)关于原点对称,则h(x)=-1+$\frac{2}{3x}$.分析 根据函数y=f(x)与函数y=-f(x)的图象关于直线x轴对称,函数y=f(x)与函数y=f(-x)的图象关于直线y轴对称,函数y=f(x)与函数y=-f(-x)的图象关于原点对称.即可得到答案.
解答 解:函数f(x)=1+$\frac{2}{3x}$的图象与y=g(x)的图象关于x轴对称,
则g(x)=-f(x)=-1-$\frac{2}{3x}$,
函数f(x)与y=h(x)关于原点对称,
则h(x)=-f(-x)=-1+$\frac{2}{3x}$,
故答案为:-1-$\frac{2}{3x}$,-1+$\frac{2}{3x}$,
点评 本题主要考查函数图象的对称变换,一般地,函数y=f(x)与函数y=-f(x)的图象关于直线x轴对称,函数y=f(x)与函数y=f(-x)的图象关于直线y轴对称,函数y=f(x)与函数y=-f(-x)的图象关于原点对称.

练习册系列答案
相关题目
10.若x>0,则-4x-$\frac{1}{x}$( )
| A. | 有最大值 | B. | 有最小值 | ||
| C. | 既无最大值又无最小值 | D. | 不确定 |
8.若I,∅分别表示全集与空集,且(∁IP)∪M?P,则集合P,M必须满足( )
| A. | ∅?P?M | B. | M?P?I | C. | M=∅ | D. | P=I且M≠P |
12.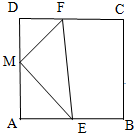 如图,在正方形ABCD中,AB=2,点E、F分别在边AB、DC上,M为AD的中点,且$\overrightarrow{ME}•\overrightarrow{MF}$=0,则△MEF的面积的取值范围为( )
如图,在正方形ABCD中,AB=2,点E、F分别在边AB、DC上,M为AD的中点,且$\overrightarrow{ME}•\overrightarrow{MF}$=0,则△MEF的面积的取值范围为( )
 如图,在正方形ABCD中,AB=2,点E、F分别在边AB、DC上,M为AD的中点,且$\overrightarrow{ME}•\overrightarrow{MF}$=0,则△MEF的面积的取值范围为( )
如图,在正方形ABCD中,AB=2,点E、F分别在边AB、DC上,M为AD的中点,且$\overrightarrow{ME}•\overrightarrow{MF}$=0,则△MEF的面积的取值范围为( )| A. | $[{1,\frac{5}{4}}]$ | B. | [1,2] | C. | $[{\frac{1}{2},\frac{5}{4}}]$ | D. | $[{\frac{1}{2},\frac{3}{2}}]$ |