题目内容
11.某公共汽车每5分钟发一次,某乘客到乘车点的时刻是随机的,则他候车时间不超过3分钟的概率$\frac{3}{5}$.分析 根据已知中某公共汽车站每隔5分钟有一辆车通过,我们可以计算出两辆车间隔的时间对应的几何量长度为5,然后再计算出乘客候车时间不超过3分钟的几何量的长度,然后代入几何概型公式,即可得到答案
解答 解:∵公共汽车站每隔5分钟有一辆车通过
当乘客在上一辆车开走后两分钟内到达候车时间会超过3分钟
∴乘客候车时间不超过3分钟的概率为
P=$\frac{5-2}{5}=\frac{3}{5}$.
故答案为:$\frac{3}{5}$
点评 本题考查的知识点是几何概型,其中计算出所有事件和满足条件的事件对应的几何量的值是解答此类问题的关键

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.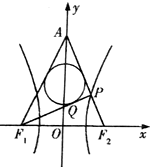 如图,已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1,F2,|F1F2|=6,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是( )
如图,已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1,F2,|F1F2|=6,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是( )
 如图,已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1,F2,|F1F2|=6,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是( )
如图,已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1,F2,|F1F2|=6,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是( )| A. | 3 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
3.已知A=N*,B={$\frac{1}{3}$,$\frac{3}{5}$,$\frac{5}{7}$,…},映射f:x→y=$\frac{2x-1}{2x+1}$(x∈A,y∈B),则在f的作用下,象$\frac{15}{17}$的原象( )
| A. | $\frac{29}{35}$ | B. | $\frac{15}{17}$ | C. | 8 | D. | 9 |
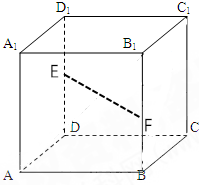 如图,在正方体ABCD-A1B1C1D1中,点E是DD1的中点,点F是BB1的中点.求证:EF∥平面ABCD.
如图,在正方体ABCD-A1B1C1D1中,点E是DD1的中点,点F是BB1的中点.求证:EF∥平面ABCD.