题目内容
9.已知两个函数f(x)=$\left\{\begin{array}{l}{{x}^{2},x≥0}\\{-{x}^{2},x<0}\end{array}\right.$,g(x)=$\left\{\begin{array}{l}{\frac{1}{x},x>0}\\{{x}^{2},x≤0}\end{array}\right.$.(1)当x≤0时,求f(g(x))的解析式;
(2)当x<0时,求g(f(x))的解析式;
(3)解不等式g(x)>2.
分析 (1)当x≤0时,判断g(x)的符号,再代入f(x)相应段上的解析式即可;
(2)当x<0时,判断f(x)的符号,再代入g(x)相应段上的解析式即可;
(3)对x进行讨论,列方程组解出.
解答 解:(1)当x≤0时,g(x)=x2≥0,
∴f(g(x))=f(x2)=(x2)2=x4.
(2)当x<0时,f(x)=-x2<0,
∴g(f(x))=g(-x2)=(-x2)2=x4.
(3)∵g(x)>2,
∴$\left\{\begin{array}{l}{x>0}\\{\frac{1}{x}>2}\end{array}\right.$或$\left\{\begin{array}{l}{x≤0}\\{{x}^{2}>2}\end{array}\right.$解得0$<x<\frac{1}{2}$或x<-$\sqrt{2}$.
即g(x)>2的解集为{x|x<-$\sqrt{2}$或0$<x<\frac{1}{2}$}.
点评 本题考查了复合函数的计算,分段函数的应用,属于中档题.

练习册系列答案
相关题目
18.已知定义在(0,+∞)上的函数f(x)的导函数为f′(x),且满足xf′(x)>2f(x),若a>b>0,则( )
| A. | b2f(a)<a2f(b) | B. | b2f(a)>a2f(b) | C. | a2f(a)<b2f(b) | D. | a2f(a)>b2f(b) |
1.已知命题p:?x∈R,都有2x≥0且x2-2x≥0,则¬p为( )
| A. | ?x∈R,都有2x≤0或x2-2x≤0 | B. | ?x0∈R,使得2x0≥0或x02-2x0≥0 | ||
| C. | ?x0∈R,使得2x0≤0且x02-2x0≤0 | D. | ?x0∈R,使得2x0<0或x02-2x0<0 |
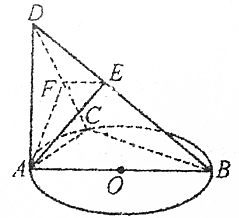 如图,AB为圆O的直径,C为圆O上的一点,AD⊥平面ABC,AE⊥BD于E,AF⊥CD于F,则BD与EF所成的角为90°.
如图,AB为圆O的直径,C为圆O上的一点,AD⊥平面ABC,AE⊥BD于E,AF⊥CD于F,则BD与EF所成的角为90°.