题目内容
用1、2、3、4、5、6、7、8组成没有重复数字的八位数,要求1与2相邻,2与4相邻,5与6相邻,而7与8不相邻.这样的八位数共有 个.(用数字作答)
考点:计数原理的应用
专题:应用题,排列组合
分析:1与2相邻,2与4相邻,有124,421两种情况,捆绑在一起,5与6相邻,捆绑在一起,当做两个元素与3进行排列,这三个元素形成四个空,把7和8在这四个位置排列,5与6内部还有一个排列,根据分步计数原理得到这种数字的总数.
解答:
解:∵1与2相邻,2与4相邻,∴有124,421两种情况,捆绑在一起,5与6相邻,捆绑在一起,当做两个元素与3进行排列有A33种结果,
这三个元素形成四个空,把7和8在这四个位置排列有A42种结果,
5与6内部还有一个排列A22,
根据分步计数原理得到这种数字的总数有2A33A42A22=288,
故答案为:288.
这三个元素形成四个空,把7和8在这四个位置排列有A42种结果,
5与6内部还有一个排列A22,
根据分步计数原理得到这种数字的总数有2A33A42A22=288,
故答案为:288.
点评:利用分步乘法计数原理,首先确定分步标准,其次满足必须并且只需连续完成这n个步骤,这件事才算完成.用两个计数原理解决计数问题时,最重要的是在开始计算之前要进行仔细分析要完成的一件事是什么,可以分类还是需要分步.

练习册系列答案
相关题目
已知i为虚数单位,a∈R,若
为纯虚数,则复数z=(2a+1)+
i的模为( )
| 2-i |
| a+i |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设等差数列{an}的前n项和为Sn,若公差d≠0,a1+a3+a5=15,a2是a1和a5的等比中项,则S9=( )
| A、49 | B、64 | C、81 | D、100 |
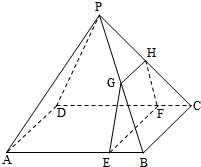 如图,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2
如图,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2