题目内容
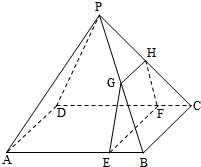 如图,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2
如图,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2| 17 |
(Ⅰ)证明:GH∥EF;
(Ⅱ)若EB=2,求四边形GEFH的面积.
考点:直线与平面垂直的性质,棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:(Ⅰ)证明GH∥EF,只需证明EF∥平面PBC,只需证明BC∥EF,利用BC∥平面GEFH即可;
(Ⅱ)求出四边形GEFH的上底、下底及高,即可求出面积.
(Ⅱ)求出四边形GEFH的上底、下底及高,即可求出面积.
解答:
 (Ⅰ)证明:∵BC∥平面GEFH,平面GEFH∩平面ABCD=EF,BC?平面ABCD,
(Ⅰ)证明:∵BC∥平面GEFH,平面GEFH∩平面ABCD=EF,BC?平面ABCD,
∴BC∥EF,
∵EF?平面PBC,BC?平面PBC,
∴EF∥平面PBC,
∵平面EFGH∩平面PBC=GH,
∴EF∥GH;
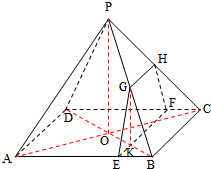
(Ⅱ)解:连接AC,BD交于点O,BD交EF于点K,连接OP,GK.
∵PA=PC,O为AC中点,
∴PO⊥AC,
同理可得PO⊥BD,
又∵BD∩AC=O,AC?底面ABCD,BD?底面ABCD,
∴PO⊥底面ABCD,
又∵平面GEFH⊥平面ABCD,PO?平面GEFH,
∴PO∥平面GEFH,
∵平面PBD∩平面GEFH=GK,
∴PO∥GK,且GK⊥底面ABCD
∴GK是梯形GEFH的高
∵AB=8,EB=2,
∴
=
=
,
∴KB=
DB=
OB,即K为OB中点,
又∵PO∥GK,
∴GK=
PO,即G为PB中点,且GH=
BC=4,
由已知可得OB=4
,PO=
=
=6,
∴GK=3,
故四边形GEFH的面积S=
(GH+EF)×GK=
(4+8)×3=18.
 (Ⅰ)证明:∵BC∥平面GEFH,平面GEFH∩平面ABCD=EF,BC?平面ABCD,
(Ⅰ)证明:∵BC∥平面GEFH,平面GEFH∩平面ABCD=EF,BC?平面ABCD,∴BC∥EF,
∵EF?平面PBC,BC?平面PBC,
∴EF∥平面PBC,
∵平面EFGH∩平面PBC=GH,
∴EF∥GH;
(Ⅱ)解:连接AC,BD交于点O,BD交EF于点K,连接OP,GK.
∵PA=PC,O为AC中点,
∴PO⊥AC,
同理可得PO⊥BD,
又∵BD∩AC=O,AC?底面ABCD,BD?底面ABCD,
∴PO⊥底面ABCD,
又∵平面GEFH⊥平面ABCD,PO?平面GEFH,
∴PO∥平面GEFH,
∵平面PBD∩平面GEFH=GK,
∴PO∥GK,且GK⊥底面ABCD
∴GK是梯形GEFH的高
∵AB=8,EB=2,
∴
| EB |
| AB |
| KB |
| DB |
| 1 |
| 4 |
∴KB=
| 1 |
| 4 |
| 1 |
| 2 |
又∵PO∥GK,
∴GK=
| 1 |
| 2 |
| 1 |
| 2 |
由已知可得OB=4
| 2 |
| PB2-OB2 |
| 68-32 |
∴GK=3,
故四边形GEFH的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查线面平行的判定与性质,考查梯形面积的计算,正确运用线面平行的判定与性质是关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设z=
+i,则|z|=( )
| 1 |
| 1+i |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
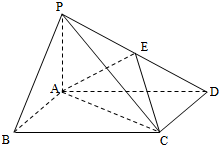 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.