题目内容
已知数列的前n项和为Sn,并且满足a1=2,nan+1=Sn+n(n+1).
(1) 求{an}的通项公式;
(2) 令Tn=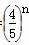 Sn,是否存在正整数m,对一切正整数n,总有Tn≤Tm?若存在,求m的值;若不存在,说明理由.
Sn,是否存在正整数m,对一切正整数n,总有Tn≤Tm?若存在,求m的值;若不存在,说明理由.
解:(1) 令n=1,
由a1=2及nan+1=Sn+n(n+1),①
得a2=4,故a2-a1=2,
当n≥2时,有(n-1)an=Sn-1+n(n-1),②
①-②,得
nan+1-(n-1)an=an+2n.
整理得an+1-an=2(n≥2).
当n=1时,a2-a1=2,所以数列{an}是以2为首项,以2为公差的等差数列,
故an=2+(n-1)×2=2n.
(2) 由(1)得Sn=n(n+1),所以Tn=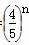 (n2+n).
(n2+n).
 解得8≤n≤9.
解得8≤n≤9.
故T1<T2<…<T8=T9>T10>T11>…
故存在正整数m对一切正整数n,总有Tn≤Tm,
此时m=8或m=9.

练习册系列答案
相关题目
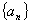 的前n项和记为Sn,已知a1=1,Sn=
的前n项和记为Sn,已知a1=1,Sn= ,(n=1,2,3,……)
,(n=1,2,3,……)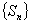 的通项公式;
的通项公式; 中,已知内角
中,已知内角 ,边
,边 ,则
,则 的最大值为 .
的最大值为 .
 ,n∈N,则a3=________.
,n∈N,则a3=________.