已知数列{an}的前n项和为Sn.3Sn＝an-1(n∈N)． (1) 求a1.a2, (2) 求证:数列{an}是等比数列, (3) 求an和Sn. 题目和参考答案——青夏教育精英家教网——

题目内容

　已知数列{a_n}的前n项和为S_n，3S_n＝a_n－1(n∈N)．

(1) 求a₁，a₂；

(2) 求证：数列{a_n}是等比数列；

(3) 求a_n和S_n.

(1) 解：由3S₁＝a₁－1，得3a₁＝a₁－1，∴ a₁＝－.

又3S₂＝a₂－1，即3a₁＋3a₂＝a₂－1，得a₂＝.

(2) 证明：当n≥2时，a_n＝S_n－S_n_－1＝(a_n－1)－(a_n_－1－1)，得＝－，所以{a_n}是首项为－，公比为－的等比数列．

(3) 解：由(2)可得a_n＝ⁿ，

S_n＝

练习册系列答案

考易通系列全国中考试题精选系列答案

鸿翔图书中考试题精选系列答案

中考汇编华语中考模拟系列答案

金榜题名新中考全程总复习系列答案

永乾教育寒假作业快乐假期延边人民出版社系列答案

新策略中考复习最佳方案同步训练系列答案

四川名校初升高自主招生一本通系列答案

北教传媒实战中考系列答案

宏翔文化寒假一本通期末加寒假加预习系列答案

总复习中考押题系列答案

相关题目

已知命题，命题，则( 　 )

A.命题是假命题 B.命题是真命题

C.命题是真命题 D.命题是假命题

已知数列的前n项和为S_n，并且满足a₁＝2，na_n_＋1＝S_n＋n(n＋1)．

(1) 求{a_n}的通项公式；

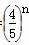(2) 令T_n＝S_n，是否存在正整数m，对一切正整数n，总有T_n≤T_m？若存在，求m的值；若不存在，说明理由．

等比数列{a_n}中，a₁>0，a₂a₄＋2a₃a₅＋a₄a₆＝36，则a₃＋a₅＝________．

已知数列{a_n}的前n项和S_n＝2n²＋2n，数列{b_n}的前n项和T_n＝2－b_n.

(1) 求数列{a_n}与{b_n}的通项公式；

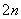(2) 设c_n＝a·b_n，证明：当且仅当n≥3时，c_n_＋1<c_n.

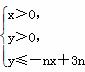已知等比数列{a_n}是递增数列，S_n是{a_n}的前n项和，若a₁，a₃是方程x²－5x＋4＝0的两个根，则S₆＝________．

数列{a_n}的首项为3，{b_n}为等差数列且b_n＝a_n_＋1－a_n(n∈N)．若b₃＝－2，b₁₀＝12，则a₈＝________．

设不等式组所表示的平面区域为D_n，记D_n内的整点个数为a_n(n∈N^*)(整点即横坐标和纵坐标均为整数的点)．

(1) 求数列{a_n}的通项公式；

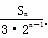(2) 记数列{a_n}的前n项和为S_n，且T_n＝.若对于一切的正整数n，总有T_n≤m，求实数m的取值范围．