题目内容
6.已知函数f(x)=2x,若存在x∈(-∞,0],使不等式f(x)+f(2x)≥m2-m成立,则实数m的取值范围是m≥2或m≤-1.分析 利用换元思想令t=2x,t≥1,得出h(x)=t2+t,由题意可知m2-m≥2,进而得出m的范围.
解答 解:若存在x∈(-∞,0],使不等式f(x)+f(2x)≥m2-m成立,
∴2x+22x≥m2-m,
令t=2x,t≥1,
h(x)=t2+t,
∴h(x)≥2,
m2-m≥2,
∴m≥2或m≤-1.
故答案为m≥2或m≤-1.
点评 考查了换元法和存在问题的求解,属于常规题型.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
1.已知点O为坐标原点,F为椭圆C:$\frac{x^2}{3}+{y^2}$=1的左焦点,点P、Q在椭圆上,点P、Q、R满足$\overrightarrow{OF}$•$\overrightarrow{PQ}$=0,$\overrightarrow{QR}$+2$\overrightarrow{PQ}$=$\overrightarrow{0}$,则$\sqrt{3}|{PF}|+|{OR}$|的最大值为( )
| A. | 6 | B. | $\sqrt{3}$(1+$\sqrt{2}$+$\sqrt{3}$) | C. | 3+3$\sqrt{2}$ | D. | 3+3$\sqrt{3}$ |
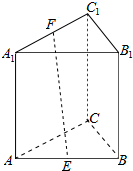 如图,正三棱柱ABC-A1B1C1的底面边长为4,侧棱长为4,E,F分别是AB,A1C1的中点,则EF的长等于2$\sqrt{5}$.
如图,正三棱柱ABC-A1B1C1的底面边长为4,侧棱长为4,E,F分别是AB,A1C1的中点,则EF的长等于2$\sqrt{5}$.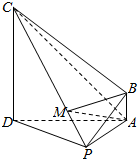 在四梭推 P-ABCD中,CD⊥平面PAD,AB∥CD,CD=4AB,AC⊥PA,M为线段CP上一点.
在四梭推 P-ABCD中,CD⊥平面PAD,AB∥CD,CD=4AB,AC⊥PA,M为线段CP上一点.