题目内容

18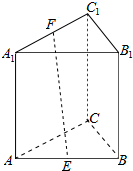．如图，正三棱柱ABC-A1B1C1的底面边长为4，侧棱长为4，E，F分别是AB，A1C1的中点，则EF的长等于2$\sqrt{5}$．

分析 由已知中正三棱柱ABC-A1B1C1（底面是正三角形的直棱柱为正三棱柱）的每条棱长均为4，E、F分别是BC、A1C1的中点，利用直线与平面垂直的性质，通过解三角形即可得到答案．

解答 解：E是BA的中点，取A1B1的中点D，连接FD，ED，
正三棱柱ABC-A1B1C1的底面边长为4，侧棱长为4，
可得ED=4，FD=2，ED⊥平面A1B1C1，|EF|=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$．
故答案为：2$\sqrt{5}$．

点评 本题考查的知识点是空间点、线、面的距离，其中建立坐标系，求出E，F两点的坐标，是解答本题的关键．

练习册系列答案
相关题目
17．若角α的正弦线的长度为$\frac{3}{4}$，且方向与y轴的正方向相反，则sinα的值为-$\frac{3}{4}$．
18．-90°+k•360°（k∈z）表示的是（　　）
A．第一象限角B．第三象限角C．界限角D．第四象限角
6．已知函数f（x）=2x，若存在x∈（-∞，0]，使不等式f（x）+f（2x）≥m2-m成立，则实数m的取值范围是m≥2或m≤-1．
13．已知函数f（x）=alnx+$\frac{1}{x}$（a≠0）．
（1）求函数f（x）的单调区间；
（2）若{x|f（x）＜0}⊆（0，e${\;}^{-\frac{1}{2}}$），求实数a的取值范围．
3．在平面直角坐标系xOy中，已知圆P在x轴上截得线段长为2$\sqrt{2}$，在y轴上截得线段长为2$\sqrt{3}$．
（Ⅰ）求圆心P的轨迹方程；
（Ⅱ）若圆心P到直线2x-y=0的距离为$\frac{\sqrt{5}}{5}$，求圆P的方程．
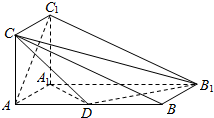10．如图，三棱柱ABC-A1B1C1的侧面AA1C1C是矩形，侧面AA1C1C⊥侧面AA1B1B，且AB=4AA1=4，∠BAA1=60°，D是AB的中点．
（Ⅰ）求证：AC1∥平面CDB1；
（Ⅱ）求证：DA1⊥平面AA1C1C．
7．某高校共有学生15000人，其中男生10500人，女生4500人．为调查该校学生每周平均体育运动时间的情况，采用分层抽样的方法，收集300位学生每周平均体育运动时间的样本数据（单位：小时）．
（Ⅰ）应收集多少位男生的样本数据？
（Ⅱ）根据这300个样本数据，得到学生每周平均体育运动时间的频率分布直方图（如图所示），其中样本数据的分组区间为[0，2]，（2，4]，（4，6]，（6，8]，（8，10]，（10，12]．估计该校学生每周平均体育运动时间超过4小时的概率；
（Ⅲ）在样本数据中有60位女生每周平均体育运动时间超过4小时，请根据独立性检验原理，判断该校学生每周平均体育运动时间与性别是否有关，这种判断有多大把握？
8．已知α∈（-$\frac{π}{2}$，0），且cosα=$\frac{\sqrt{5}}{5}$，则sin（π+2α）等于（　　）
A．$\frac{1}{5}$B．-$\frac{3}{4}$C．$\frac{4}{5}$D．-$\frac{3}{5}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网