题目内容
18.已知$\sqrt{3}$sinα+cosα=m,其中$α∈(0,\frac{π}{2})$,则实数m的取值范围是(1,2].分析 把已知等式的左边提取2后,利用特殊角的三角函数值及两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数的值域,得到左边式子的范围,进而列出关于m的不等式,求出不等式的解集即可得到m的范围.
解答 解:∵已知$\sqrt{3}$sinα+cosα=m,∴2sin(α+$\frac{π}{6}$)=m,∴sin(α+$\frac{π}{6}$)=$\frac{m}{2}$,
∵其中$α∈(0,\frac{π}{2})$,∴α+$\frac{π}{6}$∈($\frac{π}{6}$,$\frac{2π}{3}$),∴sin(α+$\frac{π}{6}$)∈($\frac{1}{2}$,1],
即$\frac{m}{2}$∈($\frac{1}{2}$,1],∴1<m≤2,
则实数m的取值范围是(1,2].
点评 此题考查了两角和与差的正弦函数公式,正弦函数的值域,以及特殊角的三角函数值,解题思路为:利用三角函数的恒等变换把已知等式左边化为一个角的正弦函数,根据正弦函数的值域列出不等式来解决问题,属于中档题.

练习册系列答案
相关题目
8.在△ABC中,内角A,B,C所对的边分别为a,b,c,A=$\frac{π}{4}$,b2-a2=c2,则tan C等于( )
| A. | 1 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
9.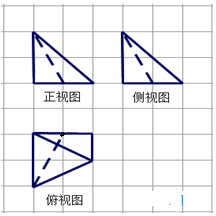 如图,网格纸上小正方形的边长为1,粗实线和虚线画出的是某空间几何体的三视图,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线和虚线画出的是某空间几何体的三视图,则该几何体的体积为( )
 如图,网格纸上小正方形的边长为1,粗实线和虚线画出的是某空间几何体的三视图,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线和虚线画出的是某空间几何体的三视图,则该几何体的体积为( )| A. | 2 | B. | $\frac{2}{3}$ | C. | 4 | D. | $\frac{4}{3}$ |
10.两条直线l1:2x+y+c=0,l2:x-2y+1=0的位置关系是( )
| A. | 平行 | B. | 垂直 | C. | 重合 | D. | 不能确定 |
8.下列函数中既是奇函数又是最小正周期为π的函数的是( )
| A. | y=|sinx| | B. | $y=cos({2x+\frac{π}{2}})$ | C. | y=sin2x+cos2x | D. | y=sinx-cosx |