题目内容
6.已知a,b,c分别为△ABC三个内角A,B,C的对边,$asinC-\sqrt{3}ccosA=0$.(1)求角A;
(2)若a=2,△ABC的面积为$\sqrt{3}$,求b,c.
分析 (1)运用正弦定理,以及同角的商数关系,结合特殊角的三角函数值,即可得到A;
(2)由余弦定理和面积公式,联立方程,即可解得b,c.
解答 解:(1)sinAsinC-$\sqrt{3}$sinCcosA=0,
∵C为三角形的内角,∴sinC≠0,
∴sinA-$\sqrt{3}$cosA=0,整理得:tanA=$\sqrt{3}$,则A=$\frac{π}{3}$;
(2)∵a=2,sinA=$\frac{\sqrt{3}}{2}$,cosA=$\frac{1}{2}$,△ABC的面积为$\sqrt{3}$,
∴$\frac{1}{2}$bcsinA=$\frac{\sqrt{3}}{4}$bc=$\sqrt{3}$,即bc①;
∴由余弦定理a2=b2+c2-2bccosA得:4=b2+c2-bc=(b+c)2-3bc=(b+c)2-12,
整理得:b+c②,联立①②解得:b=c=2.
点评 本题考查正弦定理和余弦定理、及面积公式的运用,考查三角函数的化简和求值,考查运算能力,属于中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
15.某几何体的三视图如图所示,则该几何体的表面积为( )


| A. | 36+12π | B. | 36+16π | C. | 40+12π | D. | 40+16π |
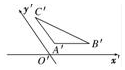 如图是三角形ABC的直观图,△ABC平面图形是直角三角形(填正三角形、锐角三角形、钝角三角形、直角三角形或者等腰三角形)
如图是三角形ABC的直观图,△ABC平面图形是直角三角形(填正三角形、锐角三角形、钝角三角形、直角三角形或者等腰三角形)