题目内容
下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是( )
A、f(x)=
| ||
| B、f(x)=x2-1 | ||
| C、f(x)=x3 | ||
| D、f(x)=2-x |
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:根据偶函数的判定方法和函数的单调性的判定方法判断即可.
解答:
解:①∵f(x)=
,
∴f(-x)=
=
=f(x),
∴f(x)=
为偶函数,但区间(0,+∞)上单调递减;
②∵f(x)=x2-1
∴f(-x)=(-x)2-1=f(x),
∴f(x)=x2-1为偶函数,
∵f(x)=x2-1开口向上,对称轴为y轴,
∴f(x)=x2-1在区间(0,+∞)上单调递增
③∵f(x)=x3,
∴f(-x)=(-x)3=-f(x)为奇函数,且再整个定义域为增函数.
④f(x)=2-x为指数函数,指数函数既不是偶函数也不是奇函数.
故选:B
| 1 |
| X2 |
∴f(-x)=
| 1 |
| (-x)2 |
| 1 |
| x2 |
∴f(x)=
| 1 |
| X2 |
②∵f(x)=x2-1
∴f(-x)=(-x)2-1=f(x),
∴f(x)=x2-1为偶函数,
∵f(x)=x2-1开口向上,对称轴为y轴,
∴f(x)=x2-1在区间(0,+∞)上单调递增
③∵f(x)=x3,
∴f(-x)=(-x)3=-f(x)为奇函数,且再整个定义域为增函数.
④f(x)=2-x为指数函数,指数函数既不是偶函数也不是奇函数.
故选:B
点评:本题考查了函数的奇偶性和单调性,属于基础题

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
若两个平面互相平行,则分别在这两个平行平面内的两条直线( )
| A、平行 | B、异面 |
| C、相交 | D、平行或异面 |
设a是实数,则“a=1”是“a2=1”的( )
| A、充分而不必要条件 |
| B、必要而不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
一个样本数据按从小到大的顺序排列为:13,14,19,x,23,27,28,32,其中,中位数是22,则x等于( )
| A、21 | B、22 | C、23 | D、24 |
(
-2x2)5的展开式中常数项是( )
| 1 | ||
|
| A、-5 | B、5 | C、-10 | D、10 |
已知函数f(x)=(1-2x3)6,则f′(1)等于( )
| A、0 | B、-6 | C、-36 | D、36 |
关于x的不等式x2-ax-6a2<0(a>0)的解集为(x1,x2),且x2-x1=10,则a=( )
| A、2 | ||
| B、5 | ||
C、
| ||
D、
|
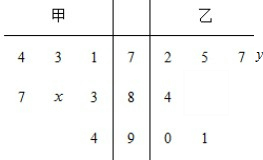 某中学高二年级的甲、乙两个班中,需根据某次数学预赛成绩选出某一班的7名学生参加数学竞赛决赛,已知这次预赛他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班7名学生成绩的平均分是81,乙班7名学生成绩的中位数是78.
某中学高二年级的甲、乙两个班中,需根据某次数学预赛成绩选出某一班的7名学生参加数学竞赛决赛,已知这次预赛他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班7名学生成绩的平均分是81,乙班7名学生成绩的中位数是78.