Question

已知平面α，β所成的二面角为80°，P为α，β外一定点，则过点P作直线与α，β都成30°的直线有（　　）

• A、1条
• B、2条
• C、3条
• D、4条

Answer 1

考点：空间中直线与直线之间的位置关系

专题：空间位置关系与距离

分析：过P作平面A垂直于α、β的交线l，并且交l于点0，连接PO，则PO垂直于l，过点P在A内做OP的垂线L'，以PO为轴在垂直于PO的平面内转动L'，根据三垂线定理可得有两条直线满足题意．以P点为轴在平面A内前后转动L'，根据三垂线定理可得也有两条直线满足题意．

解答： 解：首先给出下面两个结论
①两条平行线与同一个平面所成的角相等．
②与二面角的两个面成等角的直线在二面角的平分面上．
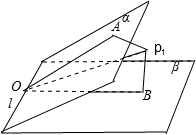图1．
（1）如图1，过二面角α-l-β内任一点作棱l的垂面AOB，交棱于点O，与两半平面于OA，OB，则∠AOB为二面角α-l-β的平面角，∠AOB=80°
设OP₁为∠AOB的平分线，则∠P₁OA=∠P₁OB=40°，与平面α，β所成的角都是30°，此时过P且与OP₁平行的直线符合要求，当OP₁以O为轴心，在二面角α-l-β的平分面上转动时，OP₁与两平面夹角变小，会对称的出现两条符合要求成30°情形．
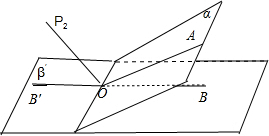图2．
（2）如图2，设OP₂为∠AOB的补角∠AOB′的平分线，则∠P₂OA=∠P₂OB=50°，与平面α，β所成的角都是50°．当OP₂以O为轴心，在二面角α-l-β′的平分面上转动时，
OP₂与两平面夹角变小，对称地在图中OP₂两侧会出现30°情形，有两条．此时过P且与OP₂平行的直线符合要求，有两条．
综上所述，直线的条数共有4条．
故选：D．

点评：本题主要考查线面角，以及考查解决线面角的特殊方法的应用，考查空间想象能力，体现了转化的思想和运动变化的思想方法，此题是个难题．