题目内容
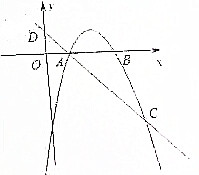 如图,已知抛物线y=ax2+bx-3(a≠0)与x轴交于A,B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,-3).
如图,已知抛物线y=ax2+bx-3(a≠0)与x轴交于A,B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,-3).(1)求抛物线解析式;
(2)点M是(1)中抛物线上一个动点,且位于直线AC的上方,试求△ACM的最大面积以及此时点M的坐标;
(3)抛物线上是否存在点P,使得△PAC是以AC为直角边的直角三角形?如果存在,求出P点的坐标;如果不存在,请说明理由.
考点:抛物线的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)代入A,C两点,列出方程,解得a,b即可;
(2)设M(a,-a2+4a-3),直线AC:y=1-x,过M作x轴的垂线交AC于N,则N(a,1-a),即有三角形ACM的面积为△AMN和△CMN的面积之和,化简运用二次函数的最值,即可得到;
(3)讨论当∠ACP=90°,当∠CAP=90°,运用直线方程和抛物线方程求交点即可.
(2)设M(a,-a2+4a-3),直线AC:y=1-x,过M作x轴的垂线交AC于N,则N(a,1-a),即有三角形ACM的面积为△AMN和△CMN的面积之和,化简运用二次函数的最值,即可得到;
(3)讨论当∠ACP=90°,当∠CAP=90°,运用直线方程和抛物线方程求交点即可.
解答:
 解:(1)由于A点的坐标是(1,0),C点坐标是(4,-3),
解:(1)由于A点的坐标是(1,0),C点坐标是(4,-3),
则a+b-3=0,且16a+4b-3=-3,解得,a=-1,b=4,
即有y=-x2+4x-3;
(2)设M(a,-a2+4a-3),直线AC:y=1-x,
过M作x轴的垂线交AC于N,则N(a,1-a),
即有三角形ACM的面积为△AMN与△CMN的面积之和,即为
(a-1+4-a)(-a2+4a-3-1+a)
=
(-a2+5a-4),当a=
时,面积取得最大,且为
,
此时M(
,
);
(3)当∠ACP=90°,即有此时CP:y=x-7,代入抛物线方程,可得,P(-1,-8);
当∠CAP=90°,即有此时AP:y=x-1,代入抛物线方程,可得,P(2,1).
故存在点P,且为(-1,-8)或(2,1),使得△PAC是以AC为直角边的直角三角形.
 解:(1)由于A点的坐标是(1,0),C点坐标是(4,-3),
解:(1)由于A点的坐标是(1,0),C点坐标是(4,-3),则a+b-3=0,且16a+4b-3=-3,解得,a=-1,b=4,
即有y=-x2+4x-3;
(2)设M(a,-a2+4a-3),直线AC:y=1-x,
过M作x轴的垂线交AC于N,则N(a,1-a),
即有三角形ACM的面积为△AMN与△CMN的面积之和,即为
| 1 |
| 2 |
=
| 3 |
| 2 |
| 5 |
| 2 |
| 27 |
| 8 |
此时M(
| 5 |
| 2 |
| 3 |
| 4 |
(3)当∠ACP=90°,即有此时CP:y=x-7,代入抛物线方程,可得,P(-1,-8);
当∠CAP=90°,即有此时AP:y=x-1,代入抛物线方程,可得,P(2,1).
故存在点P,且为(-1,-8)或(2,1),使得△PAC是以AC为直角边的直角三角形.
点评:本题考查抛物线的方程和性质,考查联立直线方程和抛物线方程,解方程求交点,考查二次函数的最值问题,属于中档题.

练习册系列答案
相关题目
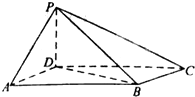 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,平面PAD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,平面PAD⊥底面ABCD.