Question

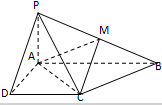如图所示，已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC=

1

2

AB，M是PB的中点
（Ⅰ）求直线AC与直线PB所成的角的余弦值；
（Ⅱ）求直线AB与面ACM所成角的正弦值．

Answer 1

考点：直线与平面所成的角,异面直线及其所成的角

专题：空间位置关系与距离,空间角

分析：由“PA⊥底面ABCD，且∠DAB=90°”可知，此题建立空间直角坐标系相当方便．以A为坐标原点，AD长为单位长度，分别以AD、AB、AP为x、y、z轴，建立空间直角坐标系，求出各点坐标计算各题．
（1）利用向量的数量积可知：cos＜

AC

，

PB

＞=

2

2 • 5

=

10

5

．可求出AC与PB所成的角余弦值．
（2）求出

AM

=（0，1，

1

2

），

AC

=（1，1，0），

AB

=（0，2，0），面ACM的法向量为

n

，运用|cos＜

n

，

AB

＞|=直线AB与面ACM所成角的正弦值求解即可．

解答： 解：以A为坐标原点AD长为单位长度，如图建立空间直角坐标系，则各点坐标为A（0，0，0），B（0，2，0），C（1，1，0），D（1，0，0），P（0，0，1），M（0，1，

1

2

）．
（1）因

AC

=（1，1，0），

PB

=（0，2，-1）
|

AC

|=

2

，|

PB

=

5

，|
所以cos＜

AC

，

PB

＞=

2

2 • 5

=

10

5

．
所以，AC与PB所成的角余弦值为

10

5

．
（2）∵M（0，1，

1

2

），

AM

=（0，1，

1

2

），

AC

=（1，1，0），

AB

=（0，2，0），
∴面ACM的法向量为

n

=（x，y，z），

n • AM =0 n • AC =0

，

x+y=0 y+ z 2 =0

，

n

=（1，-1，2），
∴cos＜

n

，

AB

＞=

-2

2× 6

=-

6

6

，
∴直线AB与面ACM所成角的正弦值

6

6

．

点评：本小题考查空间中的异面直线所成的角、二面角、解三角形等基础知识考查空间想象能力和思维能力．