题目内容
已知函数y=
(1)求函数的定义域;
(2)试判断函数在(-1,+∞)上的单调性,并给予证明;
(3)求函数在x∈[3,5]的最大值和最小值.
| 2x-1 |
| x+1 |
(1)求函数的定义域;
(2)试判断函数在(-1,+∞)上的单调性,并给予证明;
(3)求函数在x∈[3,5]的最大值和最小值.
考点:函数单调性的判断与证明,函数的定义域及其求法
专题:函数的性质及应用
分析:(1)由分母≠0求出函数的定义域;
(2)判定函数的单调性并用定义证明出来;
(3)由函数f(x)的单调性求出f(x)在[3,5]上的最值.
(2)判定函数的单调性并用定义证明出来;
(3)由函数f(x)的单调性求出f(x)在[3,5]上的最值.
解答:
解:(1)∵函数y=
,x+1≠0;
∴x≠-1,
∴函数的定义域是{x|x≠-1};
(2)∵y=f(x)=
=2-
,
∴函数f(x)在(-1,+∞)上是增函数,
证明:任取x1,x2∈(-1,+∞),且x1<x2,
则f(x1)-f(x2)=(2-
)-(2-
)
=
-
=
,
∵-1<x1<x2,
∴x1-x2<0,(x1+1)(x2+1)>0,
∴f(x1)-f(x2)<0,
即f(x1)<f(x2),
∴f(x)在(-1,+∞)上是增函数;
(3)∵f(x)在(-1,+∞)上是增函数,
∴f(x)在[3,5]上单调递增,
它的最大值是f(5)=
=
,
最小值是f(3)=
=
.
| 2x-1 |
| x+1 |
∴x≠-1,
∴函数的定义域是{x|x≠-1};
(2)∵y=f(x)=
| 2x-1 |
| x+1 |
| 3 |
| x+1 |
∴函数f(x)在(-1,+∞)上是增函数,
证明:任取x1,x2∈(-1,+∞),且x1<x2,
则f(x1)-f(x2)=(2-
| 3 |
| x1+1 |
| 3 |
| x2+1 |
=
| 3 |
| x2+1 |
| 3 |
| x1+1 |
=
| 3(x1-x2) |
| (x1+1)(x2+1) |
∵-1<x1<x2,
∴x1-x2<0,(x1+1)(x2+1)>0,
∴f(x1)-f(x2)<0,
即f(x1)<f(x2),
∴f(x)在(-1,+∞)上是增函数;
(3)∵f(x)在(-1,+∞)上是增函数,
∴f(x)在[3,5]上单调递增,
它的最大值是f(5)=
| 2×5-1 |
| 5+1 |
| 3 |
| 2 |
最小值是f(3)=
| 2×3-1 |
| 3+1 |
| 5 |
| 4 |
点评:本题考查了求函数的定义域以及判定函数的单调性、求函数的最值问题,是基础题.

练习册系列答案
相关题目
下列程序语言中表达式的值正确的是( )
| A、6*SQR(4)+3^2*2=154 |
| B、3*(5+4)+SQR(9)^2=17 |
| C、[5+3*(12-7)]/4=5 |
| D、(2+3)*5-4+2*3*SQR(4)^2=72 |
 如图,函数
如图,函数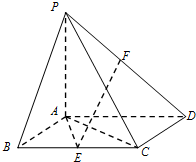 如图,已知四棱锥P-ABCD,底面ABCD为边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,PA=AB.
如图,已知四棱锥P-ABCD,底面ABCD为边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,PA=AB. 某网络营销部门为了统计某市网友2013年11月11日在某淘宝店的网购情况,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表(如表):
某网络营销部门为了统计某市网友2013年11月11日在某淘宝店的网购情况,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表(如表):