题目内容
10.己知椭圆以原点为中心,焦点在x轴上,若短半轴长为$\sqrt{3}$,椭圆的离心率为$\frac{1}{2}$.(1)求椭圆的标准方程;
(2)设椭圆的左焦点为F,直线x=m与椭圆相交于A、B两点,求当△ABF的周长最大时,△ABF的面积.
分析 (1)由题意知b=$\sqrt{3}$,a=2,c=1;从而写出椭圆的标准方程;
(2)结合题意作图,再设点A的坐标为(2cosa,$\sqrt{3}$sina)(0<a<π),从而可得|BF|=|AF|=2+cosa,|AB|=2$\sqrt{3}$sina,从而利用三角函数求最值即可.
解答 解:(1)由题意知,b=$\sqrt{3}$,e=$\frac{1}{2}$,
故a=2,c=1;
故椭圆的标准方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)结合题意作图如右,
设点A的坐标为(2cosa,$\sqrt{3}$sina)(0<a<π),
焦点F(-1,0)对应的准线方程为x=-4,
又∵e=$\frac{1}{2}$,
∴|BF|=|AF|=$\frac{1}{2}$|AC|=$\frac{1}{2}$(2cosa+4)=2+cosa,
|AB|=2$\sqrt{3}$sina,
∴△ABF的周长l=|AF|+|BF|+|AB|=4+2cosa+2$\sqrt{3}$sina
=4+4sin(a+$\frac{π}{6}$);
故当sin(a+$\frac{π}{6}$)=1,即a=$\frac{π}{3}$时,l有最大值;
此时,A(1,$\frac{3}{2}$),
此时,△ABF的面积S=2×$\frac{3}{2}$=3.
点评 本题考查了直线与圆锥曲线的位置关系的应用及三角恒等变换的应用,属于中档题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
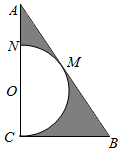 如图所示,△ABC中,∠C=90°,∠B=60°,AB=2$\sqrt{3}$,在三角形内挖去半圆(圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于N),则图中阴影部分绕直线AC旋转一周所得旋转体的内外表面积之比为$\frac{4}{9}$.
如图所示,△ABC中,∠C=90°,∠B=60°,AB=2$\sqrt{3}$,在三角形内挖去半圆(圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于N),则图中阴影部分绕直线AC旋转一周所得旋转体的内外表面积之比为$\frac{4}{9}$.