题目内容
5.已知下面四个命题①从匀速传递的产品生产流水线上,质检员每15分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②两个随机变量相关性越强,则相关系数的绝对值越接近于1;
③在回归直线方程$\widehat{y}$=0.4x+12中,当解释变量x每增加一个单位时,预报变量平均增加0.4个单位;
④对分类变量X与Y的随机变量K2的观侧值k来说,k越小,“X与Y有关系”的把握程度越大.
其中所有真命题的序号是②③.
分析 ①抽样是间隔相同,故①应是系统抽样;
②根据相关系数的公式可判断;
③由回归方程的定义可判断;
④k越小,“X与Y有关系”的把握程度越小.
解答 解:根据抽样是间隔相同,且样本间无明显差异,故①应是系统抽样,即①为假命题;
两个随机变量相关性越强,则相关系数的绝对值越接近于1;两个随机变量相关性越弱,则相关系数的绝对值越接近于0;故②为真命题;
在回归直线方程$\widehat{y}$=0.4x+12中,当解释变量x每增加一个单位时,预报变量平均增加0.4个单位,故③为真命题;
对分类变量X与Y的随机变量K2的观侧值k来说,k越小,“X与Y有关系”的把握程度越小,故④为假命题;
故答案为:②③.
点评 考查了系统抽样的概念和相关系数,回归方程定义的考查,属于基础题型,应理解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.函数f(x)的部分图象如图所示,则f(x)的解析式可以是( )
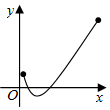

| A. | f(x)=2x+lgx+2 | B. | f(x)=2x+lgx-2 | C. | f(x)=2x-lgx+2 | D. | f(x)=2x-lgx-2 |
13.定义区间[m,n]的长度为n-m(n>m),已知函数f(x)=$\frac{({a}^{2}-2a)x-2}{{a}^{2}x}$(a∈R,a≠0)存在区间[m,n],当x∈[m,n]时,函数值域也为[m,n],则当区间[m,n]的长度最大时,a的值为( )
| A. | -3 | B. | -2 | C. | $\frac{2\sqrt{3}}{3}$ | D. | 3 |
17.在正项等比数列{an}中,若3a1,$\frac{1}{2}$a3,2a2成等差数列,则$\frac{{a}_{2016}-{a}_{2017}}{{a}_{2014}-{a}_{2015}}$=( )
| A. | 3或-1 | B. | 9或1 | C. | 3 | D. | 9 |
15.复数$\frac{2}{(1-i)i}$(i为复数单位)的共轭复数为( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
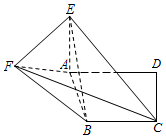 如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AE⊥平面ABCD,EF∥CD,BC=CD=AE=EF=$\frac{1}{2}$AD=1.
如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AE⊥平面ABCD,EF∥CD,BC=CD=AE=EF=$\frac{1}{2}$AD=1.