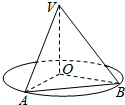
题目内容
2.已知在锐角三角形ABC中,sinA=$\frac{4}{5}$,B=$\frac{π}{4}$.(1)求cosA的值;
(2)若b=2$\sqrt{2}$,求a.
分析 (1)利用同角三角函数关系,可得结论;
(2)由正弦定理可求a.
解答 解:(1)∵锐角三角形ABC中,sinA=$\frac{4}{5}$,
∴cosA=$\frac{3}{5}$;
(2)由正弦定理可得$\frac{a}{\frac{4}{5}}=\frac{2\sqrt{2}}{\frac{\sqrt{2}}{2}}$,∴a=$\frac{8}{5}$.
点评 本题考查同角三角函数关系,正弦定理,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
13.为了研究某种细菌随时间x变化繁殖的个数,收集数据如下:
(1)用天数作解释变量,繁殖个数作预报变量,作出这些数据的散点图;
(2)求y与x之间的回归方程;
(3)计算残差、相关指数R2,并描述解释变量与预报变量之间的关系.
| 天数x/天 | 1 | 2 | 3 | 4 | 5 | 6 |
| 繁殖个数y/个 | 6 | 12 | 25 | 49 | 95 | 190 |
(2)求y与x之间的回归方程;
(3)计算残差、相关指数R2,并描述解释变量与预报变量之间的关系.
 =(2cosωx,-1),
=(2cosωx,-1),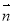 =(sinωx-cosωx,2)( ω>0),函数f(x)=
=(sinωx-cosωx,2)( ω>0),函数f(x)= 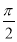 .
.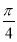 个单位,然后纵坐标不变,横坐标缩短为原来的
个单位,然后纵坐标不变,横坐标缩短为原来的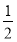 倍,得到函数g(x)的图象,当x∈[
倍,得到函数g(x)的图象,当x∈[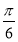 ,
,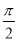 ]时,求函数g(x)的值域.
]时,求函数g(x)的值域. ,
, ,若
,若 平行,则λ=
平行,则λ= 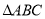 中,
中,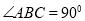 ,以
,以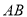 为直径的圆交
为直径的圆交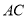 于点
于点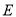 ,过点
,过点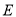 作圆
作圆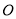 的切线交
的切线交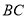 于点
于点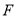 .
.
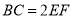 ;
;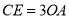 ,求
,求 的大小.
的大小.