题目内容
12.等腰三角形ABC中,AB=AC,D是AC边上中点,BD=3,则当△ABC面积最大时,∠DBC的大小为$\frac{π}{4}$.分析 建立平面直角坐标系,设出三角形的各点坐标,根据BD长度得到a,b的关系,利用基本不等式得出三角形面积的最值即三角形的边长,在△BCD中利用余弦定理求出∠DBC.
解答 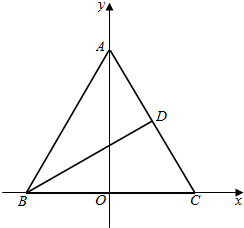 解:以BC所在直线为x轴,以BC边的高为y轴建立平面直角坐标系,设A(0,b),B(-a,0),C(a,0).
解:以BC所在直线为x轴,以BC边的高为y轴建立平面直角坐标系,设A(0,b),B(-a,0),C(a,0).
则D($\frac{a}{2}$,$\frac{b}{2}$),∴|BD|=$\sqrt{(\frac{3a}{2})^{2}+(\frac{b}{2})^{2}}$=3,整理得9a2+b2=36≥2×3ab=6ab,∴ab≤6.当且仅当3a=b时取等号.
∵S△ABC=$\frac{1}{2}×2a×b$=ab≤6.∴当3a=b时,△ABC面积取得最大值6.∴a=$\sqrt{2}$,b=3$\sqrt{2}$.
此时,BC=2a=2$\sqrt{2}$,CD=$\frac{1}{2}$AC=$\frac{1}{2}$$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{5}$.
在△BCD中由余弦定理得cos∠DBC=$\frac{9+8-5}{12\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
∴∠DBC=$\frac{π}{4}$.
故答案为$\frac{π}{4}$.
点评 本题考查了两点间的距离公式,基本不等式,余弦定理,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.一物体的运动方程是s=$\frac{1}{2}$at2(a为常数),则该物体在t=t0时的瞬时速度是( )
| A. | at0 | B. | -at0 | C. | $\frac{1}{2}$at0 | D. | 2at0 |
1.有8人已站成一排,现在要求其中4人位置不变,其余4人调换位置,则有( )种不同的调换方法.
| A. | 1680 | B. | 256 | C. | 630 | D. | 280 |