题目内容
6．下列函数的零点不能用二分法求解的是②③①y=x2-1；
②y=-x2；
③y=$\left\{\begin{array}{l}{x+1，x＜0}\\{0，x=0}\\{x-1，x＞0}\end{array}\right.$；
④y=lnx-2．
分析 根据二分法的定义，函数必须是连续函数，且函数在零点两侧的函数值异号，从而可得结论．
解答 解：①y=x2-1的零点是±1，图象穿过x轴，能用二分法求解；
②y=-x2的零点是0，图象不穿过x轴，不能用二分法求解；
③y=$\left\{\begin{array}{l}{x+1，x＜0}\\{0，x=0}\\{x-1，x＞0}\end{array}\right.$，不是连续函数，不能用二分法求解；
④y=lnx-2的零点是e2，图象穿过x轴，能用二分法求解．
故答案为：②③．
点评 本题考查二分法的定义，理解函数必须是连续函数，且函数在零点两侧的函数值异号，属于基础题．
练习册系列答案
相关题目
17．若|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2，＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=$\frac{π}{3}$，则|2$\overrightarrow{a}$$-\overrightarrow{b}$|=（ ）
| A． | 2 | B． | 2$\sqrt{3}$ | C． | 0 | D． | $\sqrt{2}$ |
14．已知R上的可导偶函数f（x）满足f（x+2）=f（x-2），又f′（1）=5，则f′（15）的值为（ ）
| A． | 5 | B． | -5 | C． | 0 | D． | ±5 |
1．函数f（x）=x+$\frac{{a}^{2}}{x}$（a＞0）的减区间为（ ）
| A． | （-a，a） | B． | （-a，0），（0，a） | C． | （-a，0）∪（0，a） | D． | 以上皆非 |
15．化简sin2β+cos4β+sin2βcos2β的结果是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | 1 | D． | $\frac{3}{2}$ |
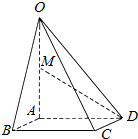如图，在四棱锥O-ABCD中，底面ABCD是边长为2的正方形，OA⊥底面ABCD，OA=2，M为OA的中点．