题目内容
10．将二进制数10110（2）化为十进制数结果为（ ）| A． | 19 | B． | 22 | C． | 44 | D． | 14 |
分析 由题意知10110（2）=0×20+1×21+1×22+0×23+1×24，计算出结果即可选出正确选项．
解答 解：10110（2）=0×20+1×21+1×22+0×23+1×24=0+2+4+16=22．
故选B．
点评 本题以进位制的转换为背景考查算法的多样性，解题的关键是熟练掌握进位制的转化规则，属于基础题．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
20．用反证法证明命题“若a2+b2=0（a，b∈R），则a，b全为0”，其反设正确的是（ ）
| A． | a，b至少有一个为0 | B． | a，b至少有一个不为0 | ||
| C． | a，b全部为0 | D． | a，b中只有一个为0 |
1．已知变量x，y的一组观测数据如表所示：
据此得到的回归方程为$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，若$\stackrel{∧}{a}$=7.9，则x每增加1个单位，y的预测值就（ ）
| x | 3 | 4 | 5 | 6 | 7 |
| y | 4.0 | 2.5 | -0.5 | 0.5 | -2.0 |
| A． | 增加1.4个单位 | B． | 减少1.4个单位 | C． | 增加1.2个单位 | D． | 减少1.2个单位 |
18．已知点F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点，过F点作双曲线的一条渐近线垂线，垂足为A，交另一条渐近线于B，若A点恰好为BF的中点，则双曲线的离心率为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | 3 |
15．如图所示，某空间几何体的正视图与侧视图相同，则此几何体的表面积为（ ）
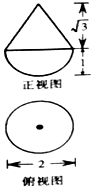
| A． | 6π | B． | $\frac{2π}{3}+\sqrt{3}$ | C． | 4π | D． | $2π+\sqrt{3}$ |
2．某品牌电动汽车的耗电量y与速度x之间满足的关系式为y=$\frac{1}{3}$x3-$\frac{39}{2}$x2-40x（x＞0），为使耗电量最小，则速度为（ ）
| A． | 30 | B． | 40 | C． | 50 | D． | 60 |
19．为了得到函数$y=4sin（2x+\frac{π}{5}），x∈R$的图象，只需把函数$y=4sin（x+\frac{π}{5}），x∈R$的图象上所有点的（ ）
| A． | 横坐标伸长到原来的2倍，纵坐标不变 | |
| B． | 纵坐标伸长到原来的2倍，横坐标不变 | |
| C． | 横坐标伸长到原来的$\frac{1}{2}$倍，纵坐标不变 | |
| D． | 纵坐标伸长到原来的$\frac{1}{2}$倍，横坐标不变 |