题目内容
3.若△PAD所在平面与矩形ABCD所在平面互相垂直,PA=PD=AB=2,∠APD=60°,若点P,A,B,C,D都在同一个球面上,则此球的表面积为( )| A. | $\frac{25}{3}$π | B. | $\frac{28}{3}$π | C. | $\frac{28\sqrt{21}}{27}$π | D. | $\frac{25\sqrt{21}}{27}$π |
分析 设球心为O,求出AD=2,BD=2$\sqrt{2}$,设AC∩BD=E,则BE=$\sqrt{2}$,OP=OB=R,设OE=x,则OB2=BE2+OE2=2+x2,过O作线段OH⊥平面PAD于H点,H是垂足,PO2=OH2+PH2=1+($\sqrt{3}$-x)2,由此能求出球半径R,由此能求出此球的表面积.
解答 解:设球心为O,如图,
∵△PAD所在平面与矩形ABCD所在平面互相垂直,PA=PD=AB=2,∠APD=60°,
∴AD=2,BD=$\sqrt{4+4}$=2$\sqrt{2}$,
设AC∩BD=E,则BE=$\sqrt{2}$,
∵点P,A,B,C,D都在同一个球面上,∴OP=OB=R,
设OE=x,在Rt△BOE中,OB2=BE2+OE2=2+x2,
过O作线段OH⊥平面PAD于H点,H是垂足,
∵O点到面PAD的距离与点E到平面PAD的距离相等,∴OH=1,
∴在Rt△POH中,PO2=OH2+PH2=1+($\sqrt{3}$-x)2=x2-2$\sqrt{3}x$+4,
∴2+x2=x2-2$\sqrt{3}x$+4,解得x=$\frac{\sqrt{3}}{3}$,∴R=$\sqrt{2+{x}^{2}}=\sqrt{2+\frac{1}{3}}=\sqrt{\frac{7}{3}}$,
∴此球的表面积S=4πR2=4π×$\frac{7}{3}$=$\frac{28}{3}π$.
故选:B.
点评 本题考查球的表面积的求法,是中档题,解题时要认真审题,注意球、四棱锥的性质及构造法的合理应用.

练习册系列答案
相关题目
18.已知集合A={2,4,6},集合B={1},则A∪B等于( )
| A. | {1,2,4,6} | B. | {0,1,8,10} | C. | {0,8,10} | D. | ∅ |
13.为防止某种疾病,今研制一种新的预防药,任选取100只小白鼠作试验,得到如下的列联表:
K2的观测值为3.2079,则在犯错误的概率不超过( )的前提下认为“药物对防止某种疾病有效”.
参考数据:
| 患病 | 未患病 | 总计 | |
| 服用药 | 15 | 40 | 55 |
| 没服用药 | 20 | 25 | 45 |
| 总计 | 35 | 65 | 100 |
参考数据:
| P( K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 0.025 | B. | 0.05 | C. | 0.010 | D. | 0.10 |

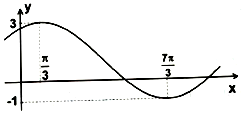 已知如图为f(x)=msin(ωx+φ)+n,m>0,ω>0的图象.
已知如图为f(x)=msin(ωx+φ)+n,m>0,ω>0的图象. 如图,六棱锥P-ABCDEF的底面是边长为1的正六边形,PA⊥底面ABCDEF.
如图,六棱锥P-ABCDEF的底面是边长为1的正六边形,PA⊥底面ABCDEF.