题目内容
18.若三棱锥P-ABC的三个侧面与底面ABC所成角都相等,则顶点P在底面的射影为△ABC的( )| A. | 外心 | B. | 重心 | C. | 内心 | D. | 垂心 |
分析 作出三个二面角,利用三角形全等得出O到△ABC的三边距离相等,得出结论.
解答  解:设P在底面ABC的射影为O,过O向△ABC的三边作垂线OD,OE,OF,
解:设P在底面ABC的射影为O,过O向△ABC的三边作垂线OD,OE,OF,
连结PD,PE,PF,
∵PO⊥平面ABC,AB?平面ABC,
∴PO⊥AB,又OD⊥AB,OD∩OP=O,
∴AB⊥平面OPD,∴AB⊥PD,
∴∠PDO为侧面PAB与平面ABC的二面角,
同理∠PEO,∠PFO为其余两侧面与底面ABC的二面角,
∴∠PDO=∠PEO=∠PFO,
又PO⊥OD,PO⊥OE,PO⊥OF,PO为公共边,
∴Rt△POD≌Rt△POE≌Rt△POF,
∴OD=OE=OF,
∴O是△ABC的内心.
故选C.
点评 本题考查了棱锥的结构特征,线面垂直的判定,二面角的做法,属于中档题.

练习册系列答案
相关题目
8.已知a=2${\;}^{-\frac{1}{3}}$,b=log${\;}_{\frac{1}{4}}$3,c=log25,则( )
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
9.从装有3个黑球和3个白球(大小、形状相同)的盒子中随机摸出3个球,用ξ表示摸出的黑球个数,则P(ξ≥2)的值为( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |
13.已知f(x)为R上的可导函数,且?x∈R,均有f(x)+f'(x)<0,则以下判断正确的是( )
| A. | e2017•f(2017)>f(0) | B. | e2017•f(2017)=f(0) | ||
| C. | e2017•f(2017)<f(0) | D. | e2017f(2017)与f(0)的大小无法确定 |
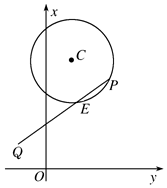 如图,已知圆C:x2+y2-4x-14y+45=0及点Q(-2,3)
如图,已知圆C:x2+y2-4x-14y+45=0及点Q(-2,3)