题目内容
设函数f(x)=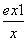 ,x≠0.
,x≠0.
(1)判断函数f(x)在(0,+∞)上的单调性;
(2)证明:对任意正数a,存在正数x,使不等式|f(x)-1|<a成立.
解析:(1)f′(x)=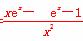 =
=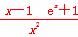 ,
,
令h(x)=(x-1)ex+1,则h ′(x)=ex+ex(x-1)=xex,
′(x)=ex+ex(x-1)=xex,
当x>0时,h′(x)=xex>0,∴h(x)是(0,+∞)上的增函数,
所以h(x)>h(0)=0,
故f′(x)=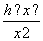 >0,即函数f(x)是(0,+∞)上的增函数.
>0,即函数f(x)是(0,+∞)上的增函数.
(2)|f(x)-1|=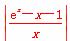 ,
,
当x>0时,令g(x)=ex-x-1,则g′(x)=ex-1>0,
故g(x)>g(0)=0,所以|f(x)-1|=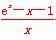 ,
,
原不等式化为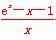 <a,即ex-(1+a)x-1<0,
<a,即ex-(1+a)x-1<0,
令φ(x)=ex-(1+a)x-1,则φ′(
 x)=ex-(1+a),
x)=ex-(1+a),
由φ′(x)=0得: ex=1+a,解得x=ln(1+a),
ex=1+a,解得x=ln(1+a),
当0<x<ln(1+a)时,φ′(x)<0;
当x>ln(1+a)时,φ′(x)>0.
故当x=ln(1+a)时,φ(x)取得最小值φ(ln(1+a))=a-(1+a)ln(1+a),
令s(a)= -ln(1+a),a>0则s′(a)=
-ln(1+a),a>0则s′(a)=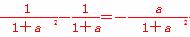 <0.故s(a)<s(0)=0,即φ(ln(1+a))=a-(1+a)ln(1+a)<0.
<0.故s(a)<s(0)=0,即φ(ln(1+a))=a-(1+a)ln(1+a)<0.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 如图,定义在[-1,+∞)上的函数f(x)的图象由一条线段及抛物线的一部分组成,求f(x)的解析式.
如图,定义在[-1,+∞)上的函数f(x)的图象由一条线段及抛物线的一部分组成,求f(x)的解析式.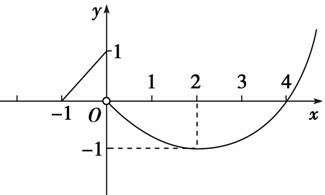
 =cos x在
=cos x在 内( )
内( ) 有一个根
有一个根 根
根 f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(-3)=0,则不等式f(x)g(x)<0的解集是________________.
f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(-3)=0,则不等式f(x)g(x)<0的解集是________________.
 1 B.(1+a)12-1
1 B.(1+a)12-1 B.a<0,4a+b=0
B.a<0,4a+b=0 结果代替sum.
结果代替sum.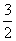 +
+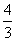 +…+
+…+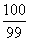 的和
的和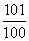 的和
的和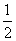 +
+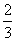 +…+
+…+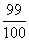 的和
的和 1+
1+ +
+ +
+