题目内容
11．
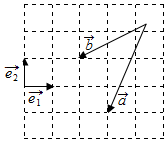如图，设$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$为互相垂直的单位向量，则向量$\overrightarrow{a}$-$\overrightarrow{b}$可表示为（ ）| A． | 2$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$ | B． | 3$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$ | C． | 2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$ | D． | $\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$ |
分析 以 $\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$为互相垂直的单位向量所在的直线分别为x轴和y轴，建立直角坐标系，求出向量$\overrightarrow{a}$的终点坐标以及$\overrightarrow{b}$的终点坐标，可得向量$\overrightarrow{a}$-$\overrightarrow{b}$的坐标，从而得到答案．
解答 解：以 $\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$为互相垂直的单位向量所在的直线分别为x轴和y轴，建立直角坐标系，
则向量$\overrightarrow{a}$的终点坐标为（3，-1），$\overrightarrow{b}$的终点坐标为（2，1），故向量$\overrightarrow{a}$-$\overrightarrow{b}$可表示为：（3，-1）-（2，1）=（1，-2）=$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$，
故选 D．
点评 本题考查两个向量的加减法的法则，以及其几何意义，两个向量坐标形式的运算，求出向量$\overrightarrow{a}$-$\overrightarrow{b}$=（1，-2），是解题的关键和难点．
练习册系列答案
相关题目
2．命题p：?k∈（0，2），直线y=kx与双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1有交点，则下列表述正确的是（ ）
| A． | p是假命题，其否定是：?k∈（2，+∞），直线y=kx与双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1有交点 | |
| B． | p是真命题，其否定是：?k∈（0，2），直线y=kx与双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1无交点 | |
| C． | p是假命题，其否定是：?k∈（0，2），直线y=kx与双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1无交点 | |
| D． | p是真命题，其否定是：?k∈（2，+∞），直线y=kx与双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1无交点 |