题目内容
已知正四面体ABCD的棱长为a．点E，F分别是棱AC，BD的中点，则
•
的值是（ ）
| AE |
| AF |
| A、a2 | ||||
B、
| ||||
C、
| ||||
D、
|
考点：平面向量数量积的运算
专题：平面向量及应用,空间向量及应用
分析：如图所示，正四面体ABCD的棱长为a．点E，F分别是棱AC，BD的中点，可得
=
(
+
)，
•
=
•
=a2cos60°．代入即可得出．
| AF |
| 1 |
| 2 |
| AB |
| AD |
| AB |
| AC |
| AD |
| AC |
解答：
解：如图所示，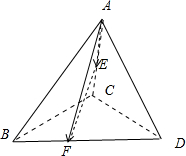
∵正四面体ABCD的棱长为a．点E，F分别是棱AC，BD的中点，
∴
=
(
+
)，
•
=
•
=a2cos60°=
a2．
∴
•
=
(
+
)•
=
(
•
+
•
)
=
×2×
a2
=
a2．
故选：C．
∵正四面体ABCD的棱长为a．点E，F分别是棱AC，BD的中点，
∴
| AF |
| 1 |
| 2 |
| AB |
| AD |
| AB |
| AC |
| AD |
| AC |
| 1 |
| 2 |
∴
| AE |
| AF |
| 1 |
| 2 |
| AB |
| AD |
| 1 |
| 2 |
| AC |
=
| 1 |
| 4 |
| AB |
| AC |
| AD |
| AC |
=
| 1 |
| 4 |
| 1 |
| 2 |
=
| 1 |
| 4 |
故选：C．
点评：本题考查了向量的平行四边形法则、数量积运算性质、正四面体的性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
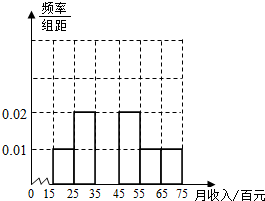为了解某市民众对某项公共政策的态度，在该市随机抽取了50名市民进行调查，做出了他们的月收入（单位：百元，范围：[15，75]）的频率分布直方图，同时得到他们月收入情况以及对该项政策赞成的人数统计表：
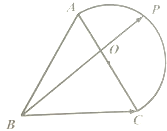已知△ABC是边长为2的正三角形，以AC为直径作半圆O（如图），P为半圆上任一点，则