题目内容
7.设集合A={x|x2-4x+3≥0},B={x|2x-3≤0},则A∪B=( )| A. | (-∞,1]∪[3,+∞) | B. | [1,3] | C. | $[{\frac{3}{2},3}]$ | D. | $({-∞,\frac{3}{2}}]∪[{3,+∞})$ |
分析 先分别求出集合A和B,由此能求出A∪B.
解答 解:∵集合A={x|x2-4x+3≥0}={x|x≤1或x≥3},
B={x|2x-3≤0}={x|x≤$\frac{3}{2}$},
∴A∪B={x|x$≤\frac{3}{2}$或x≥3}=(-∞,$\frac{3}{2}$]∪[3,+∞).
故选:D.
点评 本题考查集合的求法,是基础题,解题时要认真审题,注意并集定义和不等式性质的合理运用.

练习册系列答案
相关题目
2.已知x=1是函数f(x)=ax3-bx-lnx(a>0,b∈R)的一个极值点,则lna与b-1的大小关系是( )
| A. | lna>b-1 | B. | lna<b-1 | C. | lna=b-1 | D. | 以上都不对 |
17.如果集合A={x|ax2+4x+1=0}中只有一个元素,则a的值是( )
| A. | 0 | B. | 4 | C. | 0 或4 | D. | 不能确定 |
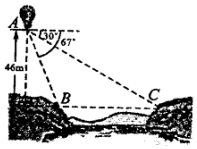 如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为67°,30°,此时气球的高是46m,则河流的宽度BC约等于60m.(用四舍五入法将结果精确到个位.参考数据:sin67°≈0.92,cos67°≈0.39,sin37°≈0.60,cos37°≈0.80,$\sqrt{3}$≈1.73.
如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为67°,30°,此时气球的高是46m,则河流的宽度BC约等于60m.(用四舍五入法将结果精确到个位.参考数据:sin67°≈0.92,cos67°≈0.39,sin37°≈0.60,cos37°≈0.80,$\sqrt{3}$≈1.73.