题目内容
若方程ax2+ay2-4(a-1)x+4y=0表示圆,求实数a的取值范围,并求出半径最小的圆的方程.
解:∵方程ax2+ay2-4(a-1)x+4y=0表示圆,∴a≠0.
∴方程ax2+ay2-4(a-1)x+4y=0可以写成
x2+y2- =0.
=0.
∵D2+E2-4F= >0恒成立,
>0恒成立,
∴a≠0时,方程ax2+ay2-4(a-1)x+4y=0表示圆.
设圆的半径为r,则
 ∴当
∴当 =
= 即,a=2时,圆的半径最小,
即,a=2时,圆的半径最小,
半径最小的圆的方程为(x-1)2+(y+1)2=2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中, 分别是
分别是 所对的边,已知
所对的边,已知 ,
, ,三角形的面积为
,三角形的面积为 ,
, 的大小; (2)求
的大小; (2)求 的值.
的值. 。
。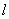 ,求与边AC,BC及
,求与边AC,BC及
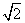 ),则四边形ABCD的面积的最大值为________.
),则四边形ABCD的面积的最大值为________. +
+ B. 18+
B. 18+ C. 18+2
C. 18+2 D. 32+
D. 32+
 的导数是:( )
的导数是:( ) B.
B.
 D.
D.