题目内容
11.已知点A(-1,0),B(3,2),则向量$\frac{1}{2}$$\overrightarrow{AB}$=( )| A. | (2,2) | B. | (-1,1) | C. | (2,1) | D. | (-4,-2) |
分析 根据平面向量的坐标表示与运算,进行化简即可.
解答 解:点A(-1,0),B(3,2),
∴向量$\overrightarrow{AB}$=(4,2),
∴$\frac{1}{2}$$\overrightarrow{AB}$=(2,1).
故选:C.
点评 本题考查了平面向量的坐标表示与运算问题,是基础题目.

练习册系列答案
相关题目
2.已知正四面体ABCD的棱长为a,其外接球表面积为S1,内切球表面积为S2,则S1:S2的值为( )
| A. | 3 | B. | $3\sqrt{3}$ | C. | 9 | D. | $\frac{49}{4}$ |
19.如图,网格纸上的小正方形边长都为4,粗线画出的是某几何体的三视图,则该几何体的体积为( )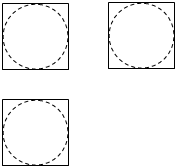

| A. | 64-$\frac{32}{3}$π | B. | 64-$\frac{96\sqrt{3}}{3}$π | C. | 64-$\frac{64\sqrt{2}}{3}$π | D. | 64-16π |
6.在等差数列{an}中,a1+a5=16,则S5=( )
| A. | 80 | B. | 40 | C. | 31 | D. | -31 |
16.某中学进行了该学年度期末统一考试,该校为了了解高一年级1 000名学生的考试成绩,从中随机抽取了100名学生的成绩单,就这个问题来说,下面说法正确的是( )
| A. | 1 000名学生是总体 | B. | 每个学生是个体 | ||
| C. | 1 000名学生的成绩是一个个体 | D. | 样本的容量是100 |
1.已知a,b,c是三条不重合的直线,α,β是两个不重合的平面,直线l∥α,则( )
| A. | a∥c,b∥c⇒a∥b | B. | a∥β,b∥β⇒a∥b | C. | a∥c,c∥α⇒a∥α | D. | a∥l⇒a∥α |
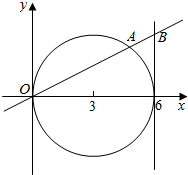 如图,已知动直线l交圆(x-3)2+y2=9于坐标原点O和点A,交直线x=6于点B;
如图,已知动直线l交圆(x-3)2+y2=9于坐标原点O和点A,交直线x=6于点B;